In trapezium ABCD, AB//DC. M is mid point of AD and N is mid-point of BC.
If AB = 5.7 cm and MN = 6.2 cm , find DC.
The correct Answer is:6.7 cm
To solve the problem, we need to find the length of side DC in trapezium ABCD where AB is parallel to DC, and M and N are the midpoints of sides AD and BC, respectively.
1. Identify the Given Information:
- AB = 5.7 cm
- MN = 6.2 cm
- M is the midpoint of AD.
- N is the midpoint of BC.
2. Use the Midsegment Theorem:
The length of the segment connecting the midpoints of the non-parallel sides (MN) in a trapezium is given by the formula:
MN=AB+DC2
Here, we need to find DC.
3. Set Up the Equation:
From the Midsegment Theorem, we can write:
6.2=5.7+DC2
4. Multiply Both Sides by 2:
To eliminate the fraction, multiply both sides by 2:
2×6.2=5.7+DC
12.4=5.7+DC
5. Isolate DC:
Now, we can isolate DC by subtracting 5.7 from both sides:
DC=12.4−5.7
6. Calculate DC:
Perform the subtraction:
DC=6.7 cm
Final Answer:
DC = 6.7 cm
- AB = 5.7 cm
- MN = 6.2 cm
- M is the midpoint of AD.
- N is the midpoint of BC.
The length of the segment connecting the midpoints of the non-parallel sides (MN) in a trapezium is given by the formula:
MN=AB+DC2
Here, we need to find DC.
From the Midsegment Theorem, we can write:
6.2=5.7+DC2
To eliminate the fraction, multiply both sides by 2:
2×6.2=5.7+DC
12.4=5.7+DC
Now, we can isolate DC by subtracting 5.7 from both sides:
DC=12.4−5.7
Perform the subtraction:
DC=6.7 cm
DC = 6.7 cm
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:pythagoras therorem
Explore 9 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Rectillinear figures
Explore 24 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Inequalities
Explore 5 Videos
- CHAPTER REVISION (STAGE 2) Book:ICSEChapter:CHAPTER REVISION (STAGE 2) Exercise:DISTANCE FORMULA
Explore 12 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:DISTANCE FORMULA
Explore 11 Videos
Similar Questions
In trapezium ABCD, AB//DC. M is mid point of AD and N is mid-point of BC.
If AB = 8 cm and DC = 11 cm , find MN.
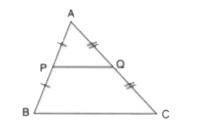
View SolutionIn triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 , find the perimeter of the trapezium PBCQ.
View SolutionIf in △ABC, AD is the bisector of ∠AandD lies on BC. If AB = 6.4 cm, AC = 8 cm, BD = 5.6 cm, find DC.
View SolutionIn the figure , given below. ABCD is a trapezium in which AB /DC , P is mid- point of AD and Q is mid-point of Bc.
Write a relations connecting AB , PQ and DC.
(ii) Find DC. If AB = 16 cm and PQ = 23 cm

View SolutionIn the adjoining figure
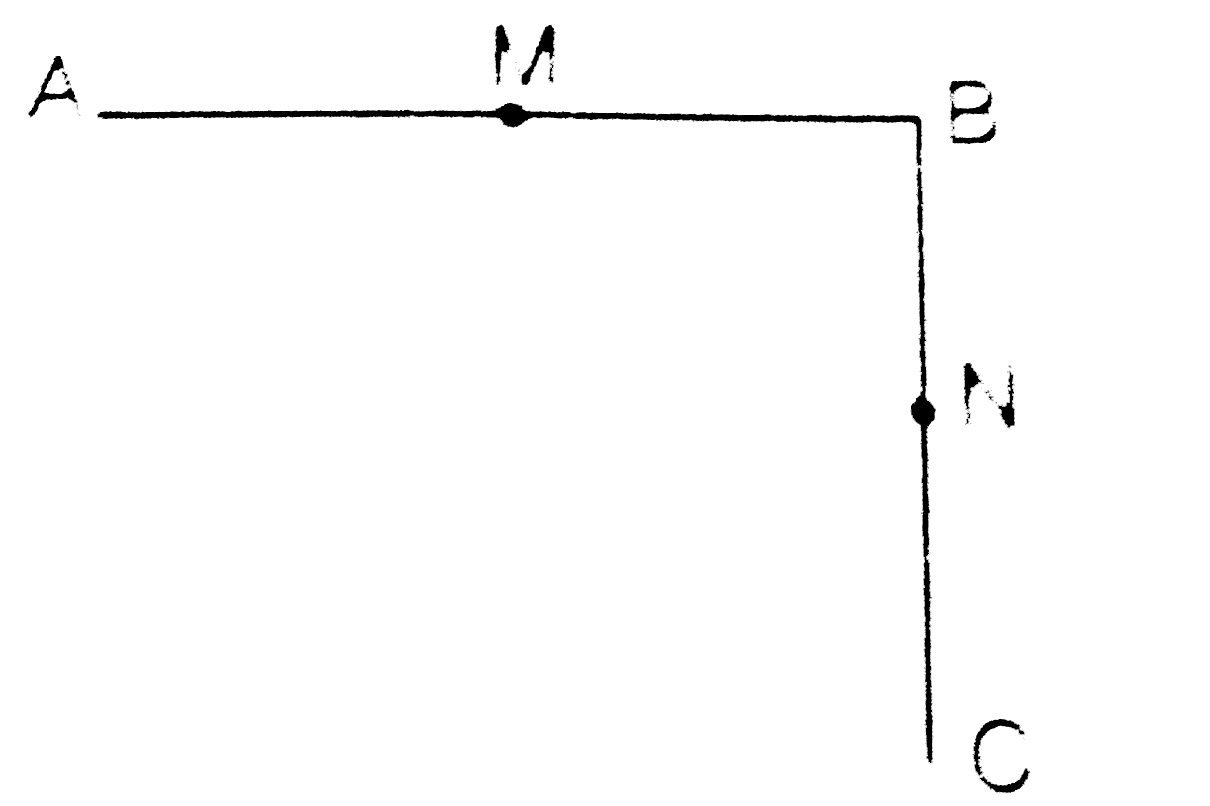
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
View SolutionIn trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that : AB + DC = 2EF.
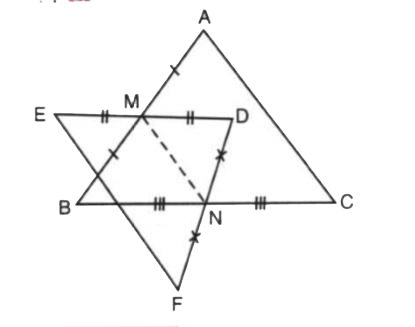
View SolutionIn the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View Solution

