The area of base of a cylindrical vessel is 300cm2. Water (density=1000kgm−3) is poured into it up to a depth of 6 cm. Calculate : (a) the pressure and (b) the thrust of water on the base. (g=10ms−2).
The correct Answer is:(a) 600 Pa (b) 18 N
To solve the problem, we will follow these steps:
Step 1: Convert the given measurements to appropriate units
- The area of the base of the cylindrical vessel is given as 300cm2. We need to convert this to square meters.
Area=300cm2=300×10−4m2=0.03m2
- The depth of water is given as 6cm. We need to convert this to meters as well.
Height=6cm=6×10−2m=0.06m
Step 2: Calculate the pressure at the depth of water
- The formula for pressure P at a certain depth in a fluid is given by:
P=density×g×h
where:
- Density of water (ρ) = 1000kg/m3
- Gravitational acceleration (g) = 10m/s2
- Height of water (h) = 0.06m
Substituting the values into the formula:
P=1000kg/m3×10m/s2×0.06m=600Pa
Step 3: Calculate the thrust of water on the base
- The thrust F on the base can be calculated using the formula:
F=P×A
where:
- Pressure P = 600Pa
- Area A = 0.03m2
Substituting the values:
F=600Pa×0.03m2=18N
Final Answers:
(a) The pressure at the depth of 6 cm is 600Pa.
(b) The thrust of water on the base is 18N.
---
- The area of the base of the cylindrical vessel is given as 300cm2. We need to convert this to square meters.
Area=300cm2=300×10−4m2=0.03m2
- The formula for pressure P at a certain depth in a fluid is given by:
- Density of water (ρ) = 1000kg/m3
- Gravitational acceleration (g) = 10m/s2
- Height of water (h) = 0.06m
- The thrust F on the base can be calculated using the formula:
- Pressure P = 600Pa
- Area A = 0.03m2
(a) The pressure at the depth of 6 cm is 600Pa.
Topper's Solved these Questions
- PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREBook:ICSEChapter:PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREExercise:Exercise-4(A)Assumptions
Explore 4 Videos
- PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREBook:ICSEChapter:PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREExercise:Exercise -4(B)
Explore 31 Videos
- PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREBook:ICSEChapter:PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREExercise:Exercise-4(A)multiple choice
Explore 4 Videos
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (C) ( Multiple choice type :)
Explore 17 Videos
- PROPAGATION OF SOUND WAVES Book:ICSEChapter:PROPAGATION OF SOUND WAVES Exercise:EXERCISE -8(B) (Multiple choice type)
Explore 3 Videos
Similar Questions
The area of base of a cylindrical vessel is 300cm2.
Water (density= 1000kg/m3) is poured into it up to a depth of 6 cm. Calculate the pressure . (g=10m s−2).
View SolutionThe area of base of a cylindrical vessel is 300cm2.
Water (density= 1000kg/m3) is poured into it up to a depth of 6 cm. Calculate the thrust of water on the base. (g=10m s−2).
View SolutionThe circumference of the base of a cylindrical vessel is 132 cm and its height is 25cm. How many litres of water can it hold?
View SolutionA vessel contains water up to a height of 1.5 m. Taking the density of water 103kgm−3, acceleration due to gravity 9.8ms−2 and area of base of vessel 100cm2 calculate : (a) the pressure and (b) the thrust, at the base of vessel.
View SolutionThe circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm.How many litres of water can it hold? (1000cm3=1l)
View SolutionA tube 1cm2 in cross- section is attached to the top of a vessel 1 cm high and of cross - section 100 cm2 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g =10 ms−2 .

View SolutionA tube 1cm2 in cross- section is attached to the top of a vessel 1 cm high and of cross - section 100 cm2 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g =10 ms−2 .

View SolutionCalculate the molarity of water if its density is 1000kgm−3
View SolutionFig. 4.11 shows a cube of each side 15 cm immersed in a tube containing water of density 103kgm−3 such that its top surface is 20 cm below the free surface of water.
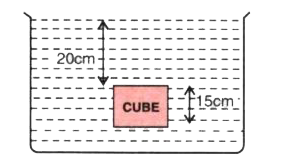
Calculate (i) the pressure at the top of cube,
(ii) the pressure at the bottom of cube,
(iii) the resultant pressure on cube.
(iv) the resultant thrust on cube.
Take atmospheric pressure = 105 Pa and g=9.8Nkg−1.
View SolutionThere is an air bubble of radius 1.0 mm in a liquid of surface tension 0.075Nm−1 and density 1000kgm−3. The bubble is at a depth of 10 cm below the free surface. By what amount is the pressure inside the bubble greater than the atmospheric pressure? Take g=9.8ms−2.
View Solution