A bulb is connected to a battery of p.d. 4 V and internal resistance 2.5 Ω. A steady current of 0.5 A flows through the circuit. Calculate :
the energy dissipated in the bulb in 10 minutes.
To solve the problem, we need to calculate the energy dissipated in the bulb when a steady current flows through it for a specified time. Here’s a step-by-step solution:
Step 1: Identify the given values
- Potential difference (V) = 4 V
- Internal resistance of the battery (r) = 2.5 Ω
- Current (I) = 0.5 A
- Time (t) = 10 minutes = 600 seconds
Step 2: Calculate the total resistance (R') of the circuit
Using Ohm's Law, the total resistance can be calculated as:
R′=VI
Substituting the values:
R′=4V0.5A=8Ω
Step 3: Calculate the resistance of the bulb (R)
The resistance of the bulb can be found by subtracting the internal resistance from the total resistance:
R=R′−r
Substituting the values:
R=8Ω−2.5Ω=5.5Ω
Step 4: Calculate the energy dissipated in the bulb
The energy (E) dissipated in the bulb can be calculated using the formula:
E=I2×R×t
Substituting the known values:
E=(0.5A)2×5.5Ω×600s
Calculating:
E=0.25×5.5×600
E=1.375×600=825Joules
Final Answer
The energy dissipated in the bulb in 10 minutes is 825 Joules.
---
- Potential difference (V) = 4 V
- Internal resistance of the battery (r) = 2.5 Ω
- Current (I) = 0.5 A
- Time (t) = 10 minutes = 600 seconds
Using Ohm's Law, the total resistance can be calculated as:
R′=VI
Substituting the values:
R′=4V0.5A=8Ω
The resistance of the bulb can be found by subtracting the internal resistance from the total resistance:
R=R′−r
Substituting the values:
R=8Ω−2.5Ω=5.5Ω
The energy (E) dissipated in the bulb can be calculated using the formula:
E=I2×R×t
Substituting the known values:
E=(0.5A)2×5.5Ω×600s
Calculating:
E=0.25×5.5×600
E=1.375×600=825Joules
The energy dissipated in the bulb in 10 minutes is 825 Joules.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:ICSEChapter:CURRENT ELECTRICITYExercise:EXERCISE-8(C) MULTIPLE CHOICE TYPE)
Explore 2 Videos
- CALORIMETRYBook:ICSEChapter:CALORIMETRYExercise:EXERCISE-11(B) (NUMERICALS)
Explore 15 Videos
- ELECTRO-MAGNETISM Book:ICSEChapter:ELECTRO-MAGNETISM Exercise:EXERCISE-10 (C) NUMERICALS
Explore 1 Video
Similar Questions
A bulb is connected to a battery of p.d. 4 V and internal resistance 2.5 Ω. A steady current of 0.5 A flows through the circuit. Calculate :
the total energy supplied by the battery in 10 minutes,
View SolutionA bulb is connected to a battery of p.d. 4 V and internal resistance 2.5 Ω. A steady current of 0.5 A flows through the circuit. Calculate :
the resistance of the bulb,
View SolutionThe circuit diagram in Fig. shows three resistors 2Ω,4Ωand RΩ connected to a battery of e.m.f. 2 V and internal resistance 3 Ω. If current of 0.25 A flows through the circuit, find :
the p.d. across the internal resistance of the cell,
View SolutionThe circuit diagram in Fig. shows three resistors 2Ω,4Ωand RΩ connected to a battery of e.m.f. 2 V and internal resistance 3 Ω. If current of 0.25 A flows through the circuit, find :
the value of R.
View SolutionThe circuit diagram in Fig. shows three resistors 2Ω,4Ωand RΩ connected to a battery of e.m.f. 2 V and internal resistance 3 Ω. If current of 0.25 A flows through the circuit, find :
the p.d. across the 4 Ω resistor,
View SolutionThe circuit diagram in Fig. shows three resistors 2Ω,4Ωand RΩ connected to a battery of e.m.f. 2 V and internal resistance 3 Ω. If current of 0.25 A flows through the circuit, find :
the p.d. across the R Ωor 2 Ω resistor,
View SolutionThree equal resistances, each of RΩ are connected as shown in figure. A battery of emf 2 V and internal resistance 0.1Ω is connected across the circuit. Calculate the value of R for which the heat generated in the circuit is maximum?
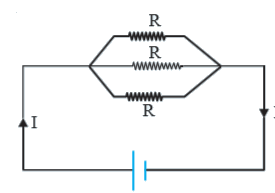
View SolutionA P-N junction diode connected to a battery of e.m.f. 4.5 V and an external resistance of 1000Ω. What is the value of current in the circuit, if potential barrier in the diode =0.5V
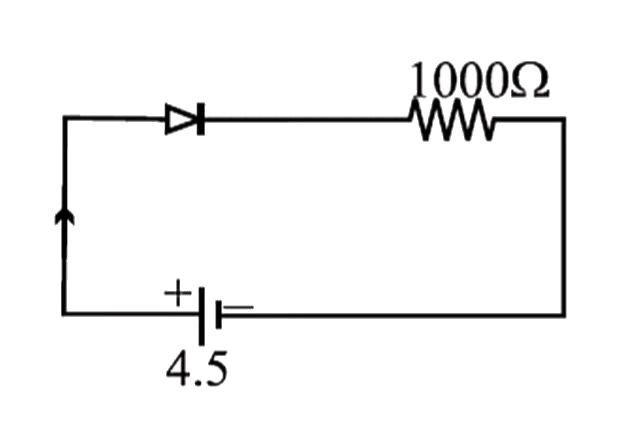
View SolutionThe internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View Solution

