A 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
Calculate the value of the resistor R, for the proper working of the lamp.
To solve the problem step by step, we will follow the logical sequence of calculations based on the information provided in the question.
Step 1: Identify the Given Values
- Voltage across the lamp, V=6V
- Power of the lamp, P=12W
- Source voltage, E=12V
Step 2: Calculate the Current through the Lamp
Using the formula for power:
P=V⋅I
We can rearrange this to find the current I:
I=PV=12W6V=2A
Step 3: Calculate the Resistance of the Lamp
Using Ohm's Law, we can find the resistance Rlamp of the lamp:
Rlamp=VI=6V2A=3Ω
Step 4: Set Up the Equation for the Total Voltage
In a series circuit, the total voltage supplied by the source is equal to the sum of the voltage drops across the lamp and the resistor R:
E=I⋅Rlamp+I⋅R
Substituting the known values:
12V=2A⋅3Ω+2A⋅R
Step 5: Simplify the Equation
12=6+2R
Step 6: Solve for the Resistor R
Rearranging the equation to solve for R:
12−6=2R
6=2R
R=62=3Ω
Conclusion
The value of the resistor R required for the proper working of the lamp is 3Ω.
---
- Voltage across the lamp, V=6V
- Power of the lamp, P=12W
- Source voltage, E=12V
Using the formula for power:
P=V⋅I
We can rearrange this to find the current I:
I=PV=12W6V=2A
Using Ohm's Law, we can find the resistance Rlamp of the lamp:
Rlamp=VI=6V2A=3Ω
In a series circuit, the total voltage supplied by the source is equal to the sum of the voltage drops across the lamp and the resistor R:
E=I⋅Rlamp+I⋅R
Substituting the known values:
12V=2A⋅3Ω+2A⋅R
12=6+2R
Rearranging the equation to solve for R:
12−6=2R
6=2R
R=62=3Ω
The value of the resistor R required for the proper working of the lamp is 3Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:ICSEChapter:CURRENT ELECTRICITYExercise:EXERCISE-8(A)
Explore 43 Videos
- CURRENT ELECTRICITYBook:ICSEChapter:CURRENT ELECTRICITYExercise:EXERCISE-8(A) ( MULTIPLE CHOICE TYPE)
Explore 2 Videos
- CALORIMETRYBook:ICSEChapter:CALORIMETRYExercise:EXERCISE-11(B) (NUMERICALS)
Explore 15 Videos
- ELECTRO-MAGNETISM Book:ICSEChapter:ELECTRO-MAGNETISM Exercise:EXERCISE-10 (C) NUMERICALS
Explore 1 Video
Similar Questions
A 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the purpose of the resistor R?
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the current flowing through the circuit?
View SolutionWhen a 12V battery is connected across an unknown resistor, there is a current of 2.5mA in the circuit. Find the value of the resistance of the resistor.
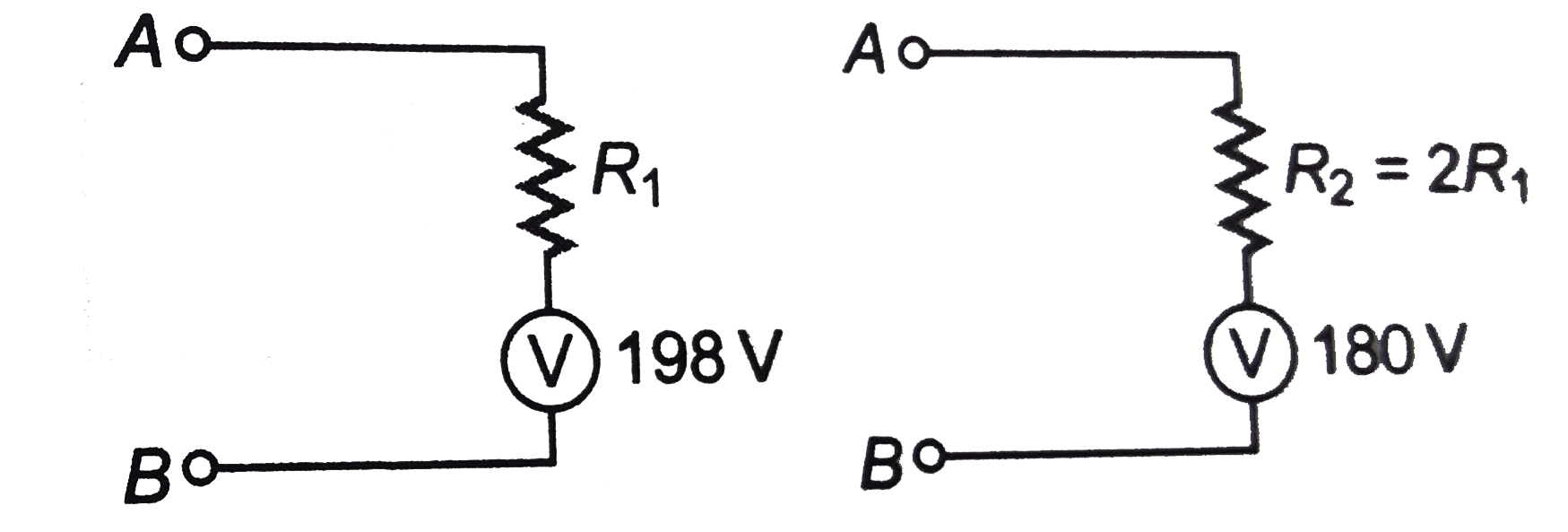
View SolutionA voltmeter connected in series with a resistance R1 to a circuit indicates a voltage V1=198V. When a series resistor R2=2R1 is used, the voltmeter indicates as voltage V2=180V. If the resistance of the voltmeter is RV=900Ω, then the applied voltage across A and B is
View SolutionA parallel combination of an 8Ω resistor and an unknown resistor R is connected in series with a 16Ω resistor and a battery. This circuit is then disassembled, and the three resistors are then connected in series with each other oand the same battery. in both arrangements, the current through the 8Ω resistor is the same. What is the unknown resistance R?

View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the current in the circuit,
View SolutionA 9/100(π) inductor and a 12Ω resistanace are connected in series to a 225 V, 50 Hz ac source. Calculate the current in the circuit and the phase angle between the current and the source voltage.
View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the potential difference across the 6 Ω resistor.
View SolutionA resistor of 200Ωand a capacitor of 15.0μF are connected in series to a 220V,50Hz source.
(a) Calculate the current in the circuit .
(b) Calcutalte the voltage (rms) across the resistor and the inductor. Is the algebraic sum of these voltages more than the source voltage? If yes, resolve the paradox.
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View Solution