A cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the p.d. across each resistor
To solve the problem, we will follow these steps:
Step 1: Draw the Circuit Diagram
We have a cell with an e.m.f. of 1.5 V and an internal resistance of 1 Ω connected to two resistors (4 Ω and 20 Ω) in series. The circuit diagram can be represented as follows:
±−−−(4Ω)−−−−(20Ω)−−−−+|∣||||(1.5V)(1Ω)|||∣±−−−−−−−−−−−−−−−−−−−−−−−−−−+
Step 2: Calculate the Total Resistance
The total resistance in the circuit (R_total) is the sum of the internal resistance and the resistances of the two resistors:
\(
R_{\text{total}} = R_1 + R_2 + r = 4 \, \Omega + 20 \, \Omega + 1 \, \Omega = 25 \, \Omega
\)
Step 3: Calculate the Current (I)
Using Ohm's Law, the current (I) flowing through the circuit can be calculated using the formula:
\(
I = \frac{E}{R_{\text{total}}}
\)
Substituting the values:
\(
I = \frac{1.5 \, \text{V}}{25 \, \Omega} = 0.06 \, \text{A}
\)
Step 4: Calculate the Potential Drop (p.d.) Across Each Resistor
Now, we will calculate the potential drop across each resistor using the formula \( V = I \times R \).
For the 4 Ω Resistor (R1):
\(
V_1 = I \times R_1 = 0.06 \, \text{A} \times 4 \, \Omega = 0.24 \, \text{V}
\)
For the 20 Ω Resistor (R2):
\(
V_2 = I \times R_2 = 0.06 \, \text{A} \times 20 \, \Omega = 1.2 \, \text{V}
\)
Step 5: Summary of Results
- The potential drop across the 4 Ω resistor is 0.24 V.
- The potential drop across the 20 Ω resistor is 1.2 V.
We have a cell with an e.m.f. of 1.5 V and an internal resistance of 1 Ω connected to two resistors (4 Ω and 20 Ω) in series. The circuit diagram can be represented as follows:
The total resistance in the circuit (R_total) is the sum of the internal resistance and the resistances of the two resistors:
R_{\text{total}} = R_1 + R_2 + r = 4 \, \Omega + 20 \, \Omega + 1 \, \Omega = 25 \, \Omega
\)
Using Ohm's Law, the current (I) flowing through the circuit can be calculated using the formula:
I = \frac{E}{R_{\text{total}}}
\)
I = \frac{1.5 \, \text{V}}{25 \, \Omega} = 0.06 \, \text{A}
\)
Now, we will calculate the potential drop across each resistor using the formula \( V = I \times R \).
\(
V_1 = I \times R_1 = 0.06 \, \text{A} \times 4 \, \Omega = 0.24 \, \text{V}
\)
\(
V_2 = I \times R_2 = 0.06 \, \text{A} \times 20 \, \Omega = 1.2 \, \text{V}
\)
- The potential drop across the 4 Ω resistor is 0.24 V.
- The potential drop across the 20 Ω resistor is 1.2 V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:ICSEChapter:CURRENT ELECTRICITYExercise:EXERCISE-8(A)
Explore 43 Videos
- CURRENT ELECTRICITYBook:ICSEChapter:CURRENT ELECTRICITYExercise:EXERCISE-8(A) ( MULTIPLE CHOICE TYPE)
Explore 2 Videos
- CALORIMETRYBook:ICSEChapter:CALORIMETRYExercise:EXERCISE-11(B) (NUMERICALS)
Explore 15 Videos
- ELECTRO-MAGNETISM Book:ICSEChapter:ELECTRO-MAGNETISM Exercise:EXERCISE-10 (C) NUMERICALS
Explore 1 Video
Similar Questions
A cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the current in the circuit,
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the voltage drop when the current is flowing.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 6 Ω resistor.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 3 Ω resistor,
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current through the battery,
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the p.d. between the terminals of the battery,
View SolutionA cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in Fig.
find : the potential difference across the 4.5 Ω resistor.
View SolutionA cell of e.m.f. 2V and internal resistance 1.2.Ω is connected with an ammeter of resistance 0.8Ω and two resistors of 4.5 Ω and 9Ω as shown in the diagram below:
What is the potential difference across the terminals of the cell?
View SolutionA battery of e.m.f. 12 V and internal resistance 2 Ω is connected with two resistors A and B of resistance 4 Ω and 6 Ω respectively joined in series.
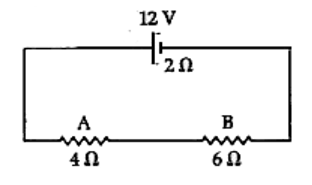
Find The potential difference across 6 Ω Resistor.
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View Solution