Find the derivatives of the following functions.
${sec}^{- 1} (\frac{l}{2 x^{2} - l}) (0 < x < \frac{l}{\sqrt{2}})$

Text Solution

Verified by Experts

The correct Answer is: $\frac{- 2}{\sqrt{l - x^{2}}}$

|

Class 11 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

$y = {sec}^{- 1} \frac{1}{2 x^{2} - 1}, 0 < x < \frac{1}{\sqrt{2}}$
View Solution
$y = {sec}^{- 1} \frac{1}{2 x^{2} - 1}, 0 < x < \frac{1}{\sqrt{2}}$
View Solution

Knowledge Check

In the following circuit find $l_{1}$ and $l_{2}$ :-

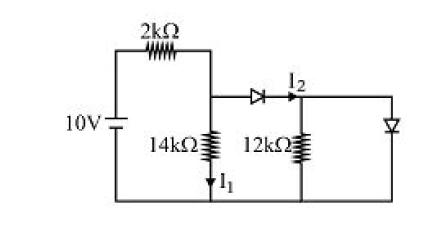A0, 0
B5 mA, 5 mA
C5 mA, 0
D0, 5 mA

VIKRAM PUBLICATION ( ANDHRA PUBLICATION)-DIFFERENTIATION-Exercise-9(c )

Home
Ask Doubt
Profile