(i) A 3μF capacitor is charged up to 300 volt and 2μF is charged up to 200 volt. The capacitor are connected so that the plates of same polarity are connected together. The final potential difference between the plates of the capacitor after they are connected is :
600
800
700
260
To solve the problem, we need to find the final potential difference across the capacitors after they are connected with the same polarity plates together. Let's break it down step by step.
Step 1: Calculate the charge on each capacitor before they are connected.
1. For the 3 µF capacitor charged to 300 V:
Q1=C1×V1=3μF×300V=900μC
2. For the 2 µF capacitor charged to 200 V:
Q2=C2×V2=2μF×200V=400μC
Step 2: Determine the total charge when the capacitors are connected.
Since the capacitors are connected with the same polarity plates together, the total charge Qtotal is the sum of the individual charges:
Qtotal=Q1+Q2=900μC+400μC=1300μC
Step 3: Calculate the equivalent capacitance when connected in parallel.
When capacitors are connected in parallel, the equivalent capacitance Ceq is the sum of their capacitances:
Ceq=C1+C2=3μF+2μF=5μF
Step 4: Find the final potential difference across the capacitors.
The final potential difference Vf across the capacitors can be found using the formula:
Vf=QtotalCeq=1300μC5μF=260V
Conclusion
The final potential difference between the plates of the capacitors after they are connected is 260 V.
---
Q1=C1×V1=3μF×300V=900μC
Q2=C2×V2=2μF×200V=400μC
Qtotal=Q1+Q2=900μC+400μC=1300μC
Ceq=C1+C2=3μF+2μF=5μF
Vf=QtotalCeq=1300μC5μF=260V
Similar Questions
Knowledge Check
The potential difference between points A and B is
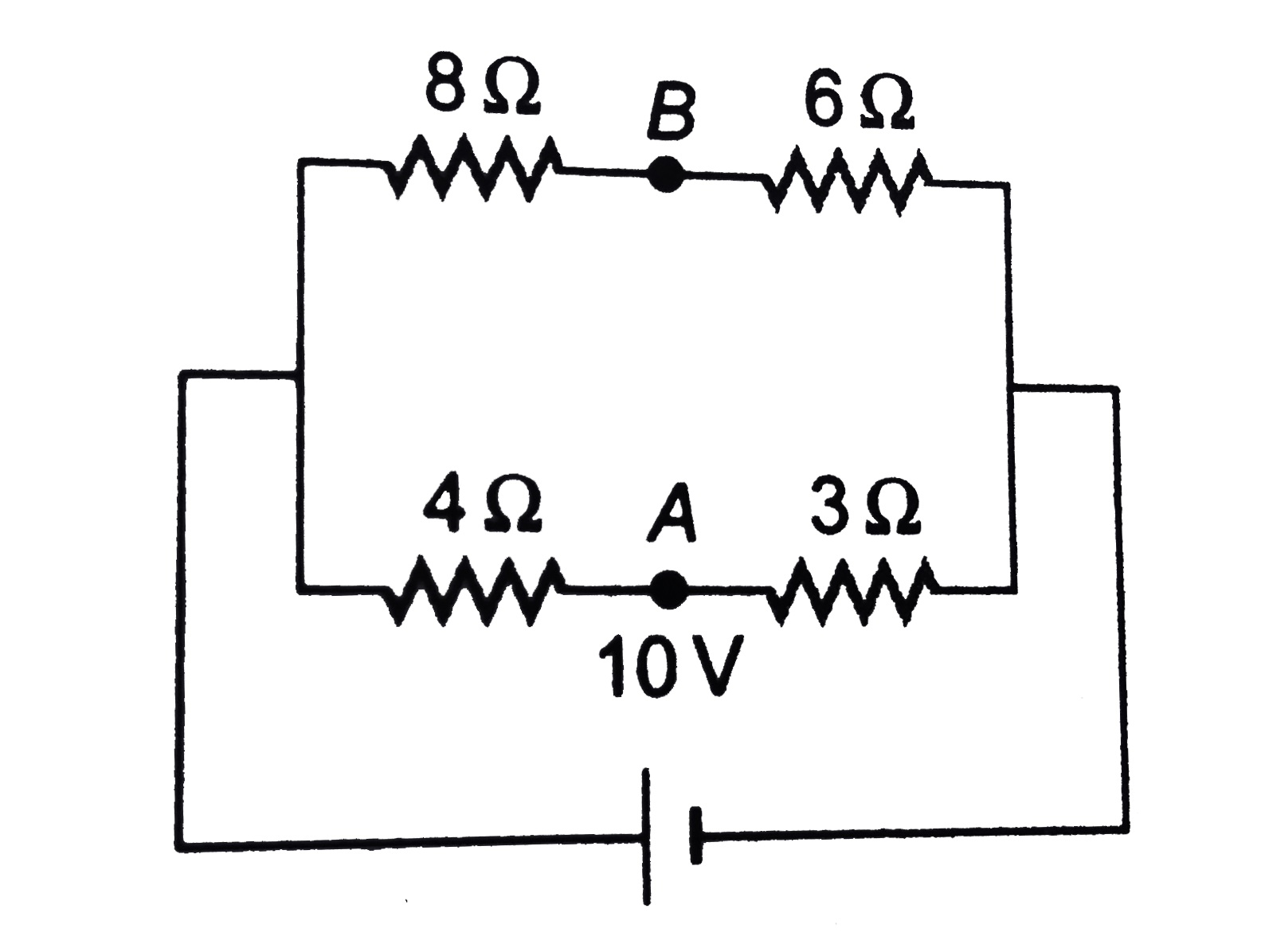 A2B5C11D18
A2B5C11D18
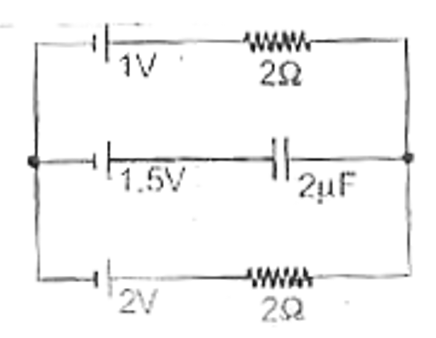
The charge in the 2μF capacitor at steady state is
View SolutionA capacity of capacity C1 is charged up to V volt and then connected to an uncharged capacitor of capacity C2. Then final potential difference across each will be
View SolutionA capacitor 4μF charged to 50V is connected to another capacitor of 2μF charged to 100V with plates of like charges connected together. The total energy before and after connection in multiples of (10−2J) is
View SolutionA capacitor of 8 F is connected as shown in the figure. At steady state Charge on the plates of the capacitor

View SolutionA capacitor having capacity of 2μF is charged to 200V and then the plates of the capacitor are connected to a resistance wire. The heat produced in joule will be
View SolutionThree capacitors of 2μF,3μF and 6μF are joined in series and the combination is charged by means of a 24 volt battery. The potential difference between the plates of the 6μF capacitor is
View SolutionTwo capacitros are fully charged by a battery as shown in the figure.
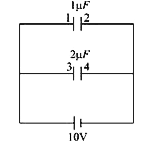
If the capacitors are disconnected from battery and plate 1 is connected to plate 4 & plate 2 to plate 3, then find the potential difference (in volts) across capacitors finally.
View Solution

_2019_CBT2_E01_002_Q01.png)