If →E equals zero at a given point mus V equal for that point .
To answer the question, "If →E=0 at a given point, must V equal for that point?", we can follow these steps:
Step 1: Understand the relationship between electric field and potential
The electric field →E is related to the electric potential V by the equation:
→E=−dVdr
This means that the electric field is the negative gradient of the electric potential.
Step 2: Analyze the condition →E=0
If the electric field →E is zero at a point, we can substitute this into the equation:
0=−dVdr
This implies that:
dVdr=0
This means that the rate of change of potential with respect to position is zero.
Step 3: Interpret the result of dVdr=0
If dVdr=0, it indicates that the potential V is constant in the vicinity of that point. However, this does not mean that the potential itself must be zero. It can take any constant value.
Step 4: Conclusion
Thus, while →E=0 implies that V is constant, it does not imply that V must equal zero. The potential could be any constant value (e.g., 0V,+5V,−2V, etc.).
Final Answer
No, if →E=0 at a given point, it does not mean that V must equal zero at that point. The potential can be any constant value.
---
The electric field →E is related to the electric potential V by the equation:
→E=−dVdr
This means that the electric field is the negative gradient of the electric potential.
If the electric field →E is zero at a point, we can substitute this into the equation:
0=−dVdr
This implies that:
dVdr=0
This means that the rate of change of potential with respect to position is zero.
If dVdr=0, it indicates that the potential V is constant in the vicinity of that point. However, this does not mean that the potential itself must be zero. It can take any constant value.
Thus, while →E=0 implies that V is constant, it does not imply that V must equal zero. The potential could be any constant value (e.g., 0V,+5V,−2V, etc.).
No, if →E=0 at a given point, it does not mean that V must equal zero at that point. The potential can be any constant value.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:EXERCISE
Explore 20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - A
Explore 44 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:SECTION-J Aakash Challengers Questions
Explore 5 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 15 Videos
Similar Questions
In figure, →E equals :
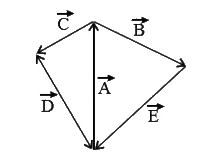
View SolutionIf you know ( E) at a given point, can you calculate V at that point ? If not, what further information do you need ?
View SolutionIf →E1 and →E2 are electric field at axial point and equatorial point of an electric dipole, then
(1) →E1.→E2>0 (2) →E1.→E2=0
(3) →E1.→E2<0 (4) →E1+→E2=→0
View Solution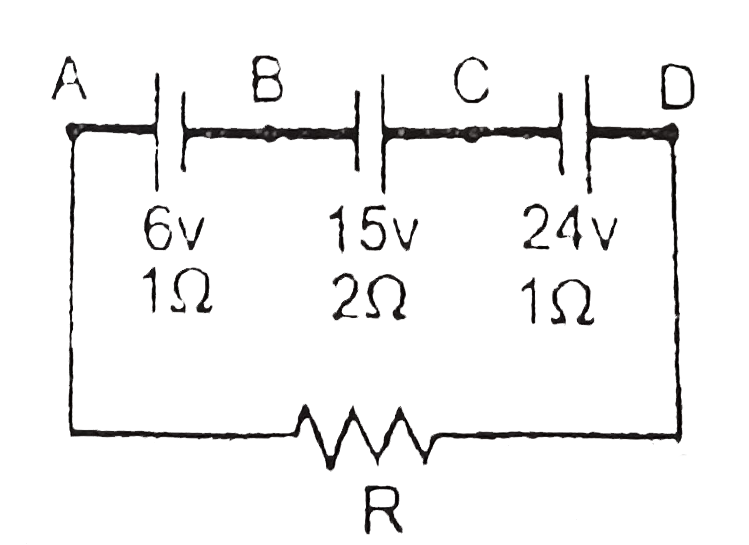
In the given circuit the point A is 9 V higher than point B.
View SolutionShow that the electric field at any point is equal to negative potential gradient at the point.
View SolutionShow that the electric field at any point is equal to negative potential gradient at the point.
View SolutionSTATEMENT-1 : At a point electrostatic field is zero, then potential at that point may be zero .
and
STATEMENT-2 : Negative of the potential gradient is equal to electrostatic field.
View SolutionFind the equation of the curve passing through the point (0, -2) given that at any point (x,y) on the curve the product of the slope of its tangent and y coordinate of the point is equal to the x-coordinate of the point.
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
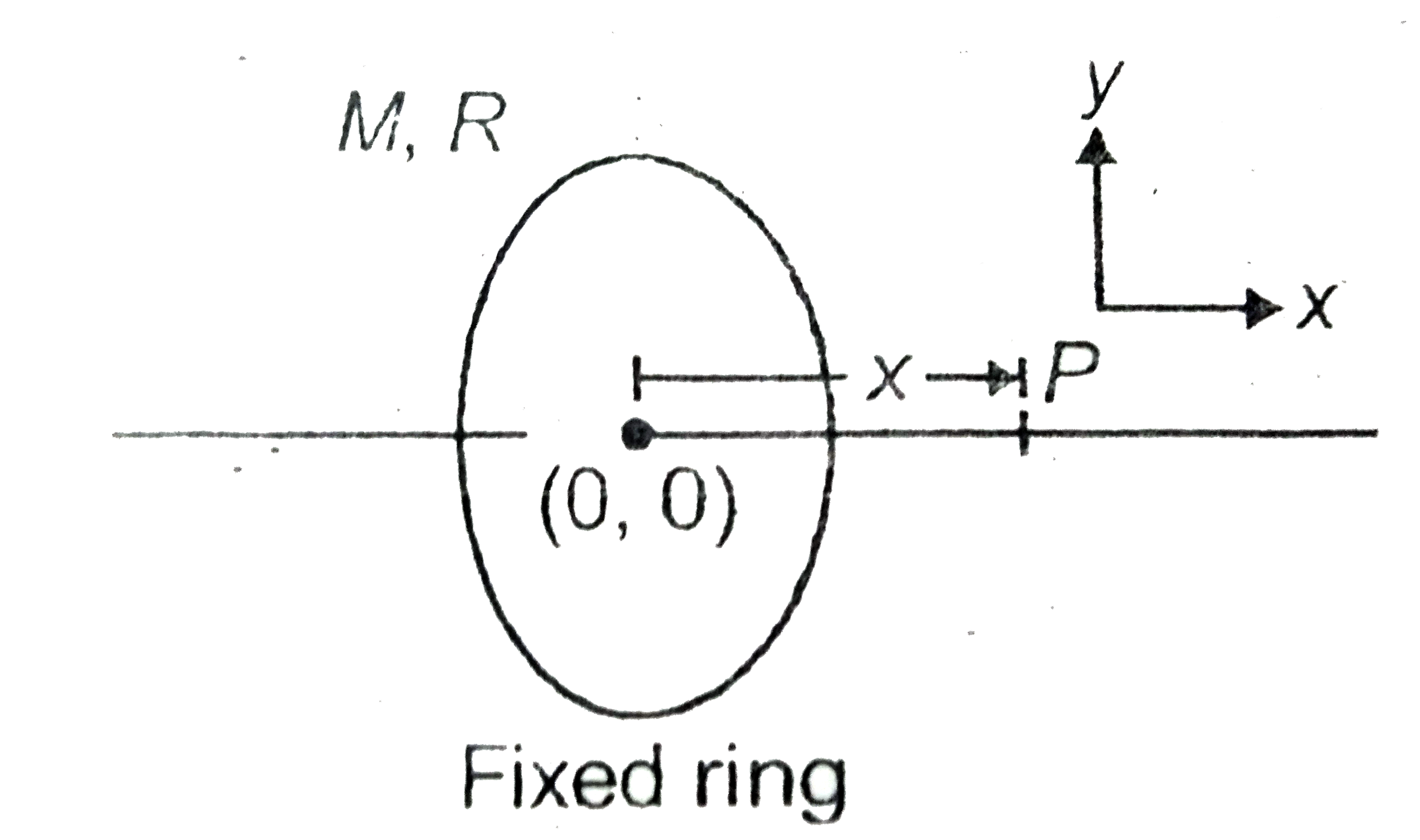
If the point mass m placed at the centre of ring and given a velocity v0 such that point mass escapes from the gravitational field of ring. Then v0 is
View SolutionA : If angular momentum of an object is constant about a point then net torque on it about that point is zero.
R : Torque is equal to the rate of change of angular momentum.
View Solution