The position (x) of a particle of mass 1 kg moving along x-axis at time t is given by (x=12t2) metre. Find the work done by force acting on it in time interval from t=0 to t=3 s.
To solve the problem of finding the work done by the force acting on a particle moving along the x-axis, we can follow these steps:
Step 1: Identify the position function
The position x of the particle is given by the equation:
x=12t2 meters
Step 2: Differentiate the position function to find velocity
To find the velocity v of the particle, we differentiate the position function with respect to time t:
v=dxdt=ddt(12t2)=12⋅2t=t meters/second
Step 3: Calculate the initial and final velocities
Now, we need to find the velocities at the specified times:
- At t=0:
v(0)=0 m/s
- At t=3:
v(3)=3 m/s
Step 4: Use the work-energy principle
The work done W by the force acting on the particle can be calculated using the change in kinetic energy:
W=ΔKE=KEfinal−KEinitial
Where the kinetic energy KE is given by:
KE=12mv2
Here, m=1 kg (mass of the particle).
Step 5: Calculate the initial and final kinetic energies
- Initial kinetic energy at t=0:
KEinitial=12⋅1⋅(0)2=0 Joules
- Final kinetic energy at t=3:
KEfinal=12⋅1⋅(3)2=12⋅1⋅9=4.5 Joules
Step 6: Calculate the work done
Now we can find the work done:
W=KEfinal−KEinitial=4.5−0=4.5 Joules
Final Answer
The work done by the force acting on the particle from t=0 to t=3 seconds is:
4.5 Joules
---
The position x of the particle is given by the equation:
x=12t2 meters
To find the velocity v of the particle, we differentiate the position function with respect to time t:
v=dxdt=ddt(12t2)=12⋅2t=t meters/second
Now, we need to find the velocities at the specified times:
- At t=0:
v(0)=0 m/s
- At t=3:
v(3)=3 m/s
The work done W by the force acting on the particle can be calculated using the change in kinetic energy:
W=ΔKE=KEfinal−KEinitial
Where the kinetic energy KE is given by:
KE=12mv2
Here, m=1 kg (mass of the particle).
- Initial kinetic energy at t=0:
KEinitial=12⋅1⋅(0)2=0 Joules
- Final kinetic energy at t=3:
KEfinal=12⋅1⋅(3)2=12⋅1⋅9=4.5 Joules
Now we can find the work done:
W=KEfinal−KEinitial=4.5−0=4.5 Joules
The work done by the force acting on the particle from t=0 to t=3 seconds is:
4.5 Joules
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
The position (x) of a particle of mass 1 kg moving along x-axis at time t is given by (x=12t2) meter. Find the work done by force acting on it in time interval from t=0 to t=3 s.
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionA particle of mass 3 kg is moving along x - axis and its position at time t is given by equation x=(2t2+5)m. Work done by all the force acting on it in time interval t=0 to t=3s is
View SolutionThe displacement x of a particle moving along x-axis at time t is given by x2=2t2+6t. The velocity at any time t is
View SolutionThe position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The velocity of the body at time t = 3s is
View SolutionThe position x of a particle moving along x - axis at time (t) is given by the equation t=√x+2, where x is in metres and t in seconds. Find the work done by the force in first four seconds
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionThe position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
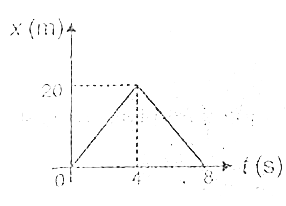
View SolutionThe position of a particle moving along x-axis is given by x=10t−2t2. Then the time (t) at which it will momentily come to rest is
View SolutionThe displacement x of a particle along the x-axis at time t is given by x=a12t+a23t2. Find the acceleration of the particle.
View Solution
