The needle of a deflection galvanometer shows a deflection of 60∘ due to a short bar magnet at a certain distance in tan A position. If the distance is doubled, the deflection is
tan−1(√23)
tan−1(√38)
tan−1(√35)
none of these
To solve the problem, we need to understand how the deflection of the galvanometer changes with distance when influenced by a bar magnet. Here’s a step-by-step solution:
Step 1: Understand the initial conditions
The initial deflection angle θ is given as 60∘ at a distance d.
Step 2: Write the formula for the magnetic field
The magnetic field H at a distance d due to a bar magnet in the tangent position is given by:
Htanθ=μ04π⋅2md3
where μ0 is the permeability of free space, and m is the magnetic moment of the bar magnet.
Step 3: Write the equation for the new distance
When the distance is doubled, the new distance d′=2d. The new deflection angle is θ′. The equation for the new deflection becomes:
Htanθ′=μ04π⋅2m(2d)3
Step 4: Simplify the new equation
Substituting d′ into the equation gives:
Htanθ′=μ04π⋅2m8d3=μ04π⋅m4d3
Step 5: Relate the two equations
Now, we can relate the two equations:
HtanθHtanθ′=μ04π⋅2md3μ04π⋅m4d3
This simplifies to:
tanθtanθ′=8d3d3=8
Thus, we have:
tanθ′=tanθ8
Step 6: Substitute the value of θ
Substituting θ=60∘, we know that:
tan60∘=√3
So,
tanθ′=√38
Step 7: Find the new deflection angle
To find θ′, we take the arctangent:
θ′=tan−1(√38)
Final Answer
The new deflection angle θ′ when the distance is doubled is:
θ′=tan−1(√38)
---
The initial deflection angle θ is given as 60∘ at a distance d.
The magnetic field H at a distance d due to a bar magnet in the tangent position is given by:
Htanθ=μ04π⋅2md3
where μ0 is the permeability of free space, and m is the magnetic moment of the bar magnet.
When the distance is doubled, the new distance d′=2d. The new deflection angle is θ′. The equation for the new deflection becomes:
Htanθ′=μ04π⋅2m(2d)3
Substituting d′ into the equation gives:
Htanθ′=μ04π⋅2m8d3=μ04π⋅m4d3
Now, we can relate the two equations:
HtanθHtanθ′=μ04π⋅2md3μ04π⋅m4d3
This simplifies to:
tanθtanθ′=8d3d3=8
Thus, we have:
tanθ′=tanθ8
Substituting θ=60∘, we know that:
tan60∘=√3
So,
tanθ′=√38
To find θ′, we take the arctangent:
θ′=tan−1(√38)
The new deflection angle θ′ when the distance is doubled is:
θ′=tan−1(√38)
Similar Questions
The tangents deflection produced in tan A and B positions by a short magnet at equal distances are in the ratio .
View SolutionTwo short magnet having magnetic moment in the ratio 27:8, when placed on the opposite sides of a deflection magnetometer, produce no deflection. If the distance of the weaker magnet is 0.12m from the centre of deflection magnetometer, the distance of the stronger magnet from the centre is
View SolutionA deflection magnetometer is placed with its arm along the east-west direction (tan A position) and a short bar magnet is placed symmetrically along its axis at some distance with its north pole pointing towards east. In this position the needle of the magnetometer shows a deflection of 60∘. If we double the distance of the bar magnet, then the deflection will be
View SolutionThe needle of a deflection magnetometer deflects through 45∘ from north to south when the instrument is used in Tan-A position with a magnet of length 10cm placed at a distance of 25cm. (a) Find the magnetic moment of the magnet if the earth's horizontal magnetic field is 20μT. (b) If the magnetometer is used in Tan−B position with the same magnet at the same separation from the needle, what will be the deflection?
View SolutionThe magnetic needle of a tangent galvanometer is deflected at an angle 30∘ due to a magnet. The hoeizontal component of earth's magnetic field 0.34×10−4T is along the plane of the coil. The magnetic intensity is
View SolutionFor the following diagram the galvanometer shows zero deflection then what is the value of R?
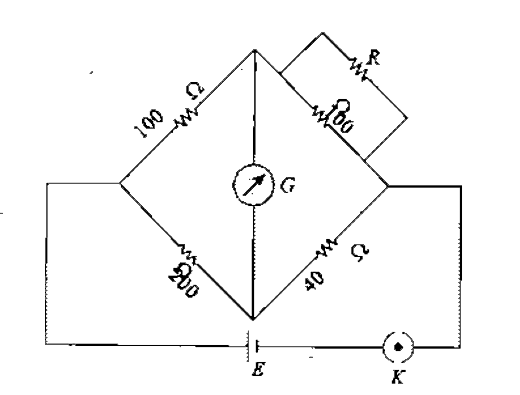
View SolutionThe ratio of the magnetic fields due to small bar magnet in end position and on broad side position is (at equal distance from the magnet)
View SolutionThe ratio of the magnetic fields due to small bar magnet in end position an broad side on position is (at equal distance from the magnet)
View SolutionThe magnetic field at a distance d from a short bar magnet in longitudinal and transverse positions are in the ratio.
View SolutionIn a circuit for finding the resistance of a galvanometer by half deflection method, a 6 V battery and a high resistance of 11 kΩ are used. The figure of merit of the galvanometer is 60 μA/division. In the absence of shunt resistance, the galvanometer produces a deflection of θ=9 divisions when current flows in the circuit. The value of the shunt resistance that can cause the deflection of θ/2, is closet to :
View Solution
