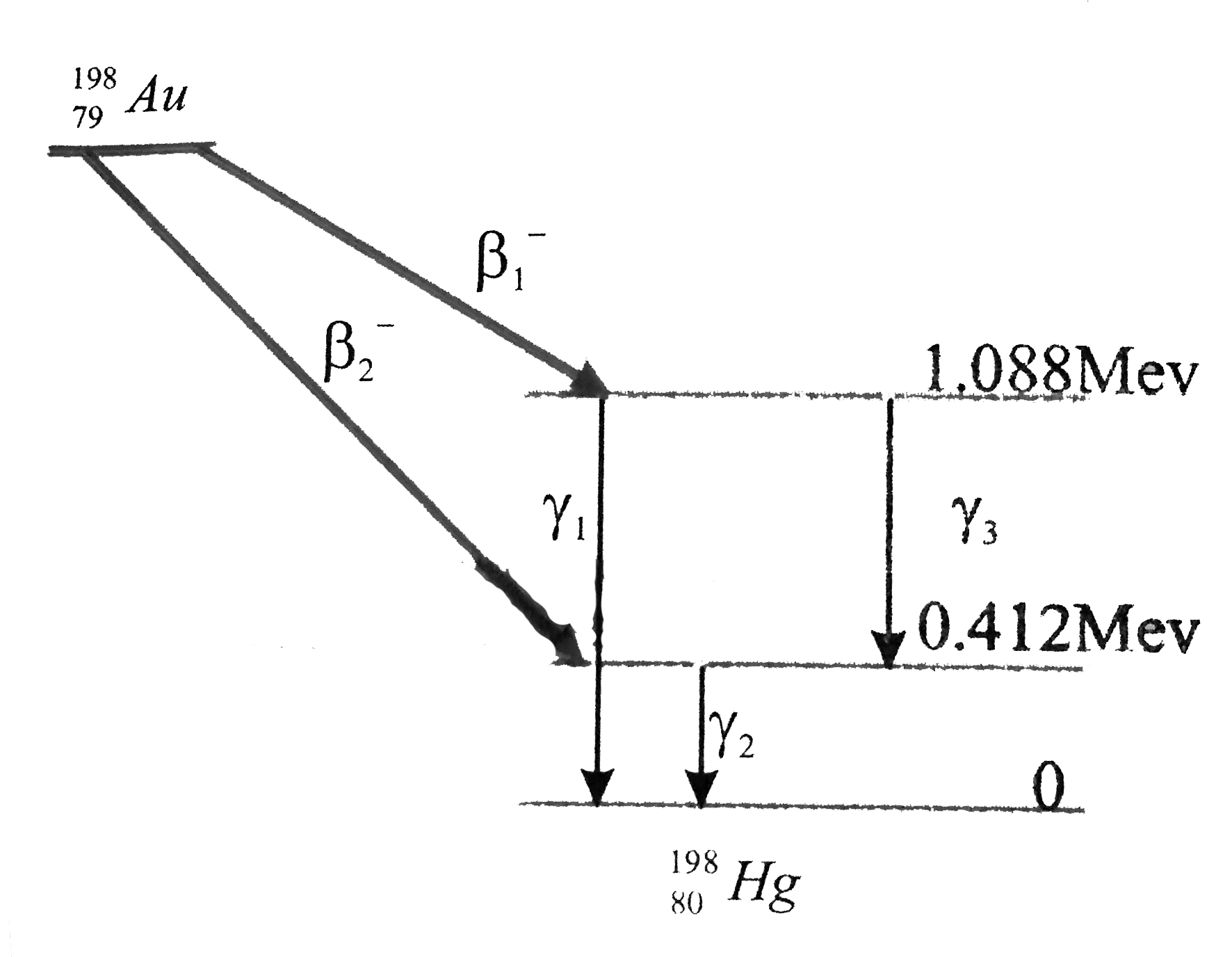
Calculate the kinetic energy of $β$ -particles and the radiation frequencies corresponding to the $γ$ -decays shown in figure.
Given, mass of $._{12} M g^{27}$ atom =26.991425 amu and mass of $._{13} A l^{27}$ atom = 26.990080 amu

Video Solution

Text Solution

Verified by Experts

Energy of photon $v_{1}, h v_{1} = \frac{E_{3} - E_{2}}{h} = \frac{(1.015 - 0.834) M e V}{6.62 \times 10^{- 34} J s}$
$\frac{0.181 \times 1.6 \times 10^{- 13} J}{(6.62 \times 10^{- 34} J s) = 4.37 \times 10^{19} s^{- 1}}$
Energy of photon $v_{2}, v_{2} = \frac{E_{3} - E_{1}}{h} = \frac{(1.015 - 0) M e V}{6.62 \times 10^{- 34} J s} = 2.45 \times 10^{20} s^{- 1}$
Energy of photon $v_{3}, v_{3} = \frac{E_{3} - E_{1}}{h} = \frac{(0.834 - 0) M e V}{6.62 \times 10^{- 34}} = 2.0 \times 10^{20} s^{- 1}$
Now emission of $β_{1}^{-}$ particle is given by $_{12} M g^{27} \to_{13} A I^{27} + β^{-} + v_{2} + Q$
$Q = [m (_{12} M g^{27}) - m (_{13} A I^{27}) - E (v_{2})$
$= [26.991425 - 26.990080] u - (E_{3} - E_{1}) M e V$
$= 0.001345 \times 931 - 1.015 M e V$
$∴$ K.E of $β_{2}^{-}$ particle is given by $_{12} M g^{27} \to_{13} A I^{27} + β_{2}^{-} + v_{3} + Q$
$= {[26.991425 - 26.990080] 931 - 0.34} M e V$
=0.418 MeV

Updated on:21/07/2023

|

Class 12 PHYSICS NUCLEI

Topper's Solved these Questions

Similar Questions

AAKASH INSTITUTE ENGLISH-NUCLEI-ASSIGNMENT (SECTION-D)

Home
Ask Doubt
Profile