If the intensity of an X-ray becomes I03 from I0 after travelling 3.5cm inside a target then its intensity after travelling next 7 cm will be
I06
I012
I09
I027
To solve the problem step by step, we will use the formula for the intensity of X-rays as they travel through a material. The formula is:
I=I0e−μx
where:
- I is the intensity after traveling distance x,
- I0 is the initial intensity,
- μ is the absorption coefficient,
- x is the distance traveled.
Step 1: Determine the absorption coefficient from the first distance
We know that after traveling 3.5 cm, the intensity becomes I03.
Using the formula:
I03=I0e−3.5μ
Dividing both sides by I0:
13=e−3.5μ
Taking the natural logarithm of both sides:
ln(13)=−3.5μ
This implies:
3.5μ=−ln(13)=ln(3)
Thus, we have:
μ=ln(3)3.5
Step 2: Calculate the intensity after traveling the next 7 cm
Now we need to find the intensity after traveling an additional 7 cm. The total distance traveled will be 3.5+7=10.5 cm.
Using the intensity formula again:
I=I0e−10.5μ
We can express e−10.5μ as:
e−10.5μ=e−3.5μ⋅e−7μ
From our previous calculation, we know:
e−3.5μ=13
Now we need to find e−7μ:
e−7μ=e−3.5μ⋅e−3.5μ=(e−3.5μ)2=(13)2=19
Thus, we can write:
I=I0⋅e−10.5μ=I0⋅(13)⋅(19)
This simplifies to:
I=I0⋅127
Final Result
Therefore, the intensity after traveling the next 7 cm will be:
I=I027
- I is the intensity after traveling distance x,
- I0 is the initial intensity,
- μ is the absorption coefficient,
- x is the distance traveled.
Similar Questions
Knowledge Check
Light from two coherent sources of the same amplitude A and wavelength λ illuminates the screen. The intensity of the central maximum is I0. If the sources were incoherent, the intensity at the same point will be
A4I0B2I0CI0DI02In Young's double slit experiment, the slits are horizontal. The intensity at a point P as shown in figure is 34I0,whereI0 is the maximum intensity.
Then the value of θ is,
(Given the distance between the two slits S1 and S2 is 2λ)
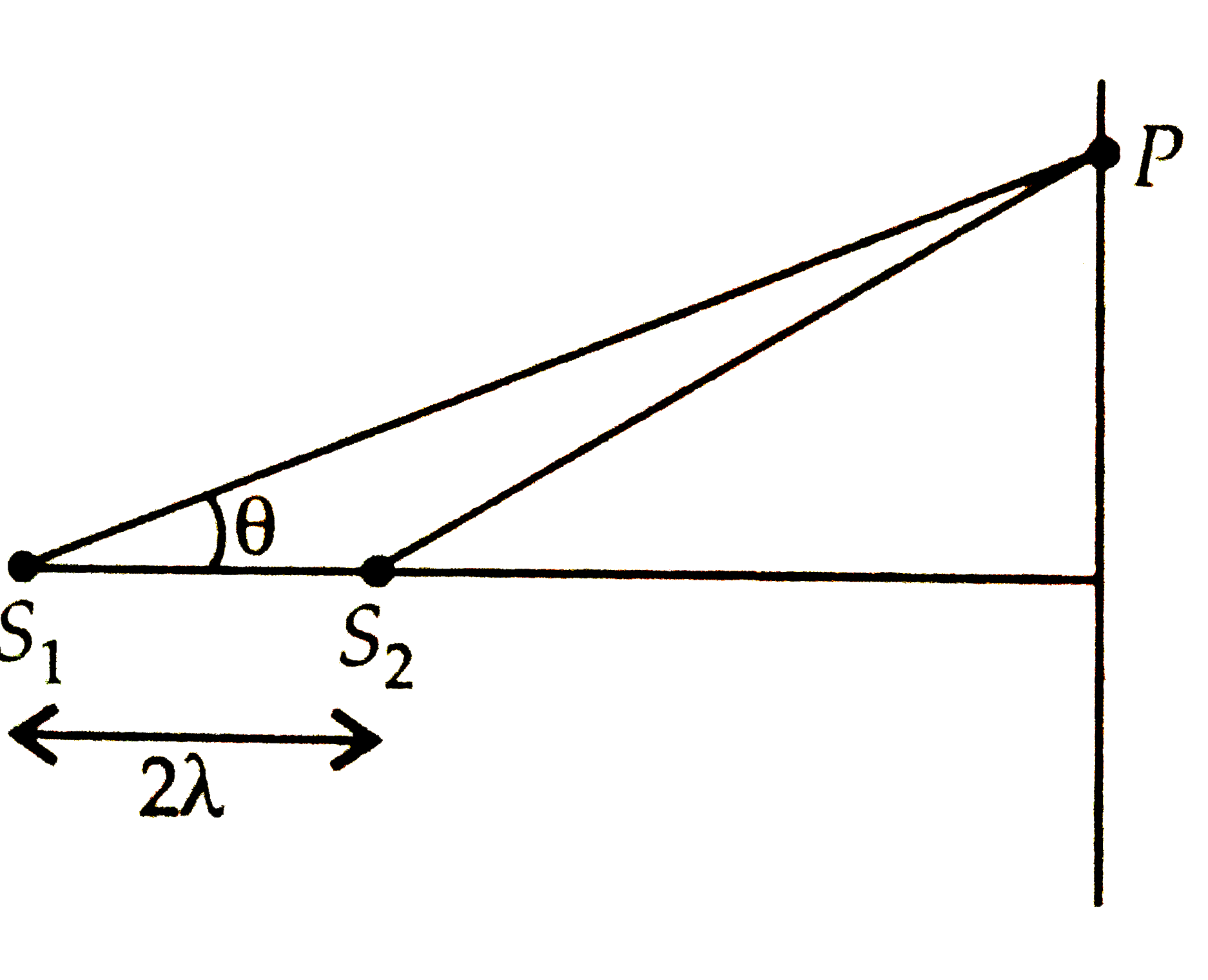 Acos−1(112)Bsin−1(112)Ctan−1(112)Dsin−1(35)
Acos−1(112)Bsin−1(112)Ctan−1(112)Dsin−1(35)
Assertion Two coherent sources transmit waves of equal intensity I0 Resultant intensity at a point where path difference is λ3 is also I0.
Reason In interference resultant intensity at any point is the average intensity of two individual intensities.
View SolutionFour harmonic waves of equal freuencies and equal intensity I0 have phase angles 0,π3,2π3 and π. When they are superposed, the intensity of the resulting wave is nI0. The value of n is
View SolutionIf I0 is the intensity of the principal maximum in the single slit diffraction pattern. Then what will be its intensity when the slit width is doubled?
View SolutionLight is incident on a polarizer with intensity I0. A second prism called analyzer is kept at a angle of 15∘, from the first polarizer then the intensity of final emergent light will be

View SolutionA ray of light is incident on the hypotenuse of a right-angled prism after travelling parallel to the base inside the prism. If μ is the refractive index of the material of the prism, the maximum value of the base angle for which light is totally reflected from the hypotenuse is
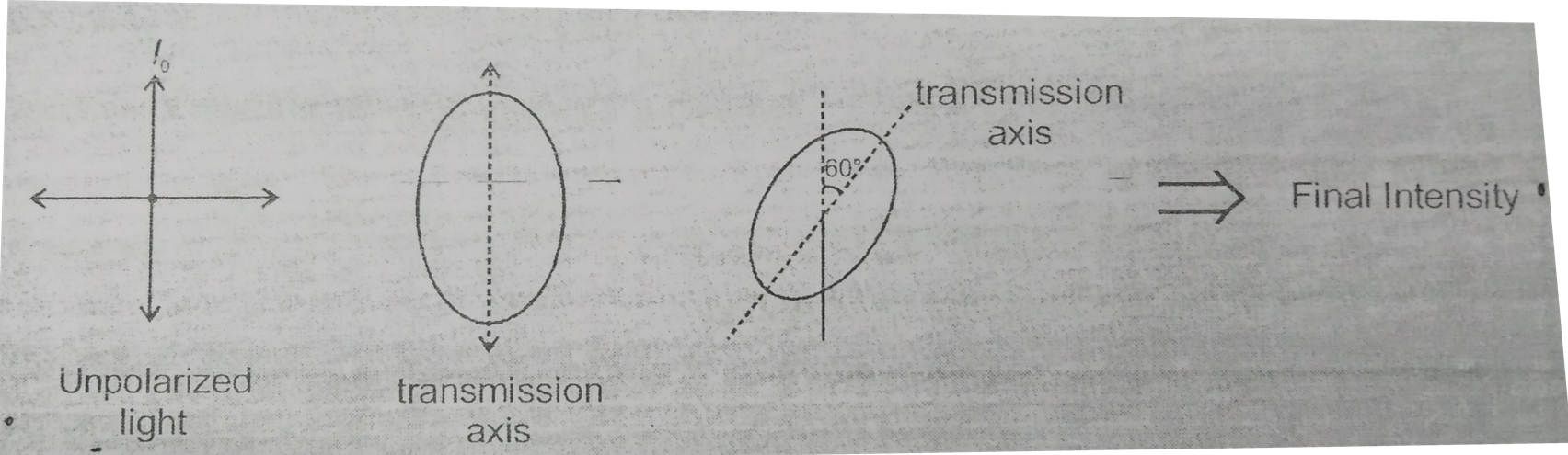
View SolutionUnpolarized light with intensity I0 is incident on combination of two polarizers as shown . The intensity of the light after passage through both the polaroids will be.
View Solution
