An infinite line charge produces a field of 9×104NC at a distance of 2cm. Calculate the linear charge density.
Use, E=λ2πε0r=2λ4πε0r
or, 9×104(N/C)=9×109×2λ0.02
∴Λ=10−7 coulomb per metre
Similar Questions
An infinite line charge produces a field of 9×10−4NC−1 at a distance of 2 cm. Calculate the linear charge density.
View SolutionAn infinite line charge Produces a field of 9x104NC−1 at a distance of 3 cm. Calculate the linear charge density.
View SolutionAn infinite line charge produces a field of 18×104 N/C at a distance of 2 metre from it. The linear charge density is
View SolutionAn infinite line charge produces a field of 7.182×108N/C at distance of 2 cm. the linear charge density is
View SolutionTwo infinite linear charges are placed parallel to each other at a distance 0.1m from each other. If the linear charge density on each is 5μC/m, then the force acting on a unit length of each linear charge will be:
View SolutionAn electric dipole consists of charges ±2.0×10−8 C separated by distance of ±2.0×10−3m. It is placed at a distance of 6 cm from a line charge of linear charge density 4.0×10−4Cm−1 as shown in figure such that the dipole makes an angle of θ=60∘ with line AB. Find the force acting on the dipole.
 View Solution
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
_2019_CBT2_E01_009_Q01.png) View Solution
View SolutionA positive charge is released from rest at a distance r0 from a positive line charge with uniform density . The speed (v) of the point charge , as a function of instantaneous distance r from line charge, is proportional to:
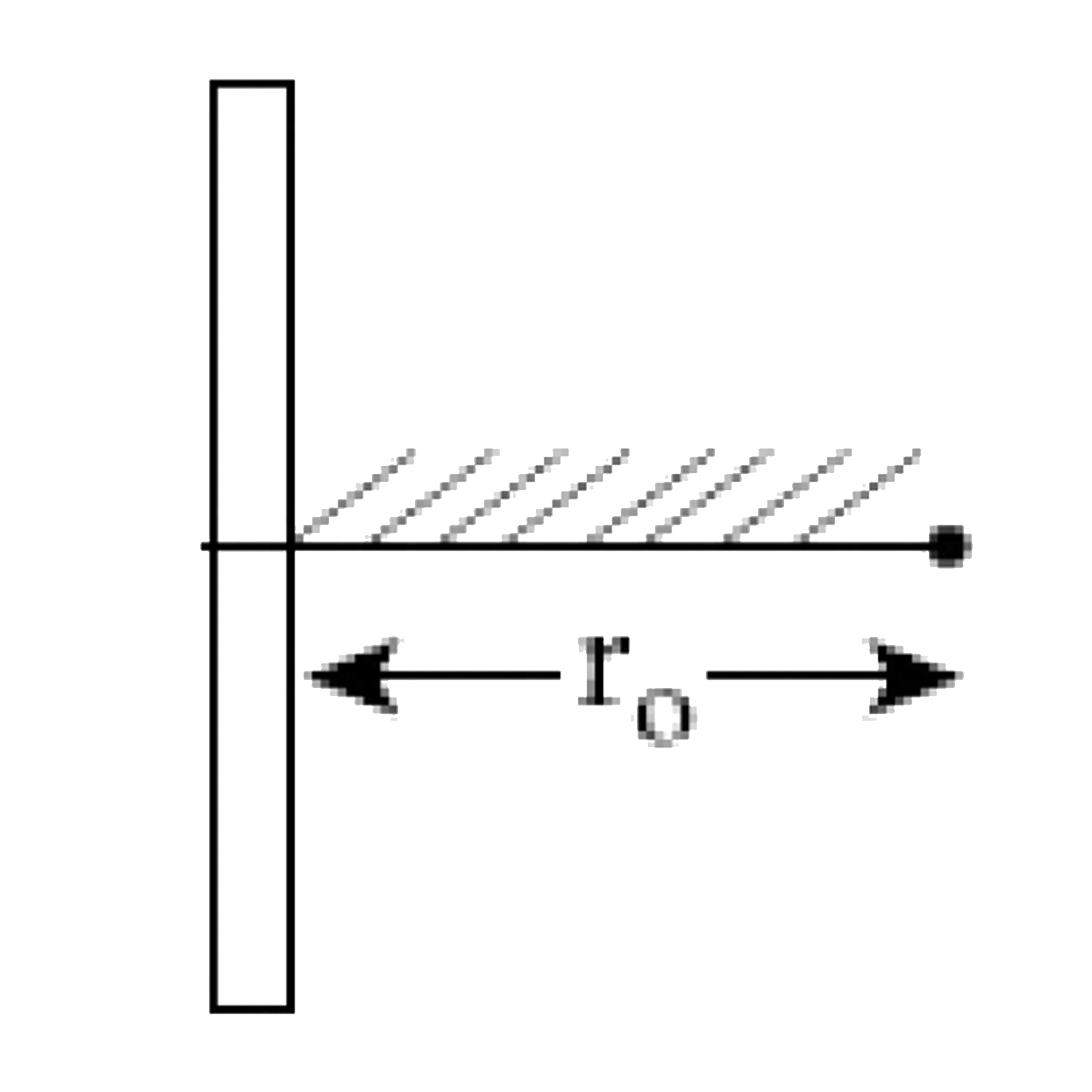 View Solution
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionAn electric dipole consists of charges ±2.0×10−8C separated by a distance of 2.0×10−3 m. It is placed near a long line charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such that the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.
 View Solution
View Solution
