A force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about origin?
To find the torque acting on a particle about the origin due to a force, we can use the formula for torque:
Torque(τ)=r×F
where:
- r is the position vector from the point about which we are calculating the torque to the point where the force is applied.
- F is the force vector.
1. Identify the Force Vector:
The force acting on the particle is given as:
F=^i−2^j+3^k
2. Determine the Position Vector:
Since the particle is located at the origin, the position vector r is:
r=0^i+0^j+0^k=0
3. Calculate the Torque:
Using the torque formula:
τ=r×F
Substitute r and F:
τ=0×(^i−2^j+3^k)
4. Evaluate the Cross Product:
The cross product of the zero vector with any vector is always the zero vector:
τ=0
5. Conclusion:
Therefore, the torque acting on the particle about the origin is:
τ=0
Final Answer:
The torque acting on the particle about the origin is the zero vector, 0.
---
- r is the position vector from the point about which we are calculating the torque to the point where the force is applied.
- F is the force vector.
The force acting on the particle is given as:
F=^i−2^j+3^k
Since the particle is located at the origin, the position vector r is:
r=0^i+0^j+0^k=0
Using the torque formula:
τ=r×F
Substitute r and F:
τ=0×(^i−2^j+3^k)
The cross product of the zero vector with any vector is always the zero vector:
τ=0
Therefore, the torque acting on the particle about the origin is:
τ=0
The torque acting on the particle about the origin is the zero vector, 0.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions
13 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about the origin.
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle of position vector (3ˆi+2ˆj+ˆk). Calculate the torque acting on the particle.
View SolutionA force (2ˆi+3ˆj−ˆk) newtons acts on a particle having position vector (ˆi−ˆj+2ˆk) . Find the torque of the force about origin.
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle of position vector (3ˆi+2ˆj+ˆk). Calculate the ˆjth component of the torque acting on the particle.
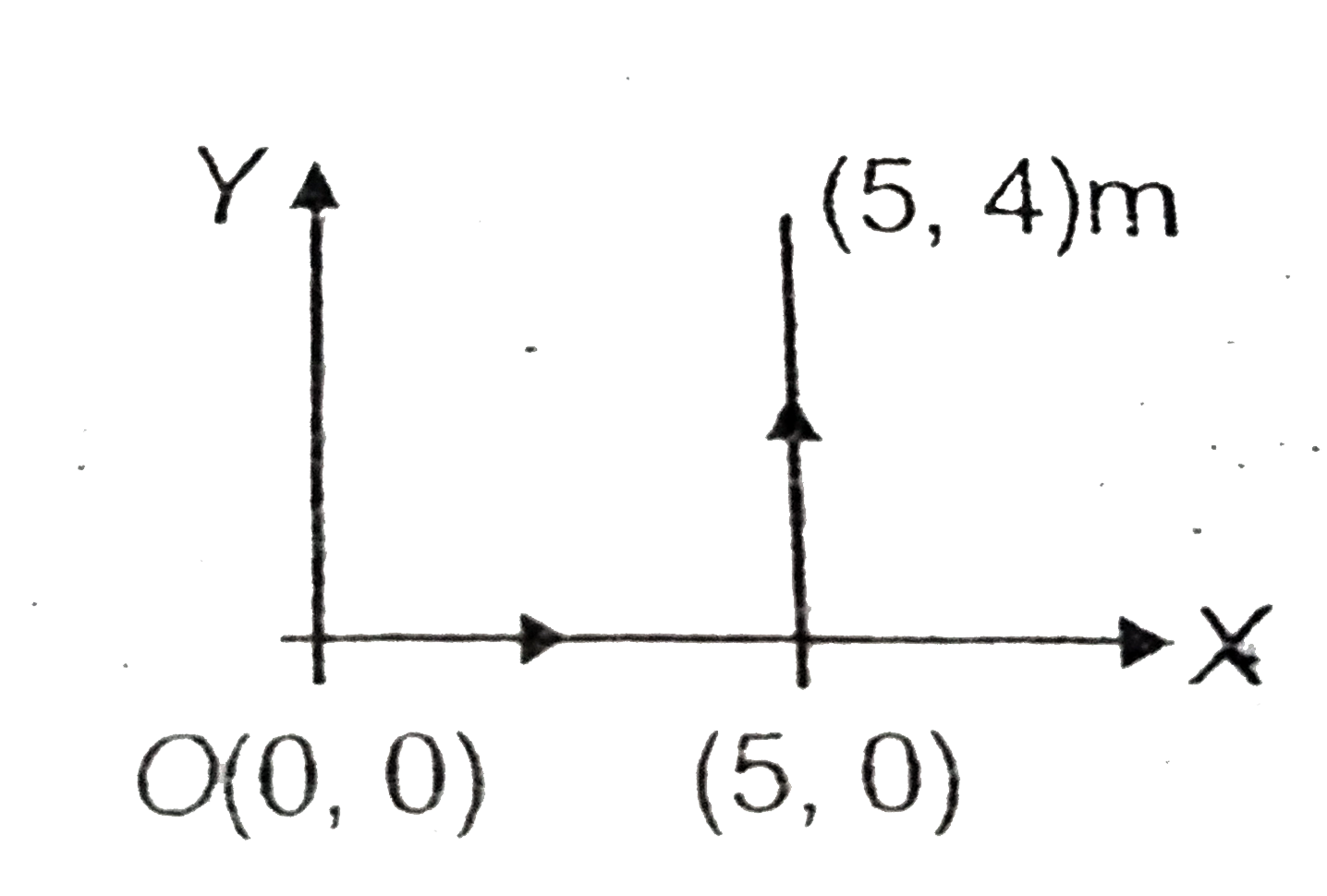
View SolutionA force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View SolutionA force (2ˆi+3ˆj−ˆk) newtons acts on a particle having position vector (ˆi−ˆj+2ˆk) . Find the torque of the force about origin.
View SolutionWork done by a force F=(ˆi+2ˆj+3ˆk) acting on a particle in displacing it from the point r1=ˆi+ˆj+ˆk to the point r2=ˆi−ˆj+ˆ2k is
View SolutionThree forces ˆi+2ˆj−3ˆk,2ˆi+3ˆj+4ˆkandˆi−ˆj+ˆk acting on a particle at the point (0,1,2) the magnitude of the moment of the forces about the point (1,-2,0) is
View SolutionA particle of mass m is released in vertical plane from a point P at x=x0 on the x-axis. It falls vertically parallel to the y-axis. Find the torque τ acting on the particle at a time about origin.

View SolutionA force F=(2ˆi+3ˆj−2ˆk)N is acting on a body at point (2m, 4m,−2m). Find torque of this force about origin.
View Solution
