Question

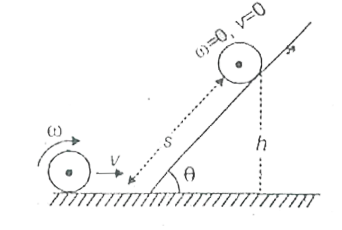
A solid sphere is rolling without slipping on a level surface at a constant speed of $2m{s}^{-1}$. How far can it roll up a ${30}^{\circ }$ ramp before its stops ?

Explanation

The moment of inertia of the sphere about its axis of rotaion is `l=(2)/(5)mr^(2)`
Suppose it rises to height h before stopping. Using the conservation of energy, we get
`mgh = (1)/(2)mv^(2)+(1)/(2)l omega^(2)=(1)/(2)mv^(2)+(1)/(2)((2)/(5)mr^(2))omega^(2)`
`= (1)/(2)mv^(2)+(1)/(5)mv^(2)=(7)/(10)mv^(2)`
or `h=(7v^(2))/(10 g)`
`therefore` The distance rolled up on the ramp is
`s=(h)/(sin theta)=(7v^(2))/(10g sin theta)=(7(2ms^(-1))^(2))/(10(0.8ms^(-2))xx(1)/(2))`
`= (4)/(7)` metre = 57 cm.