A metal rod of length 50cm having mass 2kg is supported on two edges placed 10cm from each end. A 3kg load is suspended at 20cm from one end. Find the reactions at the edges (take g=10m/s2)
To solve the problem step by step, we will analyze the forces and torques acting on the metal rod.
Step 1: Understand the Setup
- The metal rod has a length of 50 cm (0.5 m) and a mass of 2 kg.
- The rod is supported at two edges, which are 10 cm (0.1 m) from each end.
- A 3 kg load is suspended at a distance of 20 cm (0.2 m) from one end.
Step 2: Calculate the Weights
- Weight of the rod (W1):
W1=mass×g=2kg×10m/s2=20N
- Weight of the suspended load (W2):
W2=mass×g=3kg×10m/s2=30N
Step 3: Set Up the Equilibrium Equation
Since the rod is in equilibrium, the sum of the upward forces (reactions at the edges) must equal the sum of the downward forces (weights):
RA+RB=W1+W2
Substituting the values:
RA+RB=20N+30N=50N(1)
Step 4: Calculate the Torque About Point A
We will take moments about point A to find the reaction at point B (R_B). The distances from point A to the weights are:
- Distance to W1 (weight of the rod) = 15 cm (0.15 m) from A (since the center of the rod is at 25 cm or 0.25 m from one end).
- Distance to W2 (suspended load) = 20 cm (0.2 m) from A.
- Distance to R_B = 30 cm (0.3 m) from A.
Setting the sum of torques about point A to zero:
W2×0.2+W1×0.15−RB×0.3=0
Substituting the weights:
30N×0.2+20N×0.15−RB×0.3=0
Calculating the left side:
6+3−0.3RB=0
9=0.3RB
RB=90.3=30N(2)
Step 5: Substitute Back to Find R_A
Now, substitute RB back into equation (1):
RA+30N=50N
RA=50N−30N=20N(3)
Final Answers
- Reaction at edge A, RA=20N
- Reaction at edge B, RB=30N
- The metal rod has a length of 50 cm (0.5 m) and a mass of 2 kg.
- The rod is supported at two edges, which are 10 cm (0.1 m) from each end.
- A 3 kg load is suspended at a distance of 20 cm (0.2 m) from one end.
- Weight of the rod (W1):
W1=mass×g=2kg×10m/s2=20N
- Weight of the suspended load (W2):
W2=mass×g=3kg×10m/s2=30N
Since the rod is in equilibrium, the sum of the upward forces (reactions at the edges) must equal the sum of the downward forces (weights):
RA+RB=W1+W2
Substituting the values:
RA+RB=20N+30N=50N(1)
We will take moments about point A to find the reaction at point B (R_B). The distances from point A to the weights are:
- Distance to W1 (weight of the rod) = 15 cm (0.15 m) from A (since the center of the rod is at 25 cm or 0.25 m from one end).
- Distance to W2 (suspended load) = 20 cm (0.2 m) from A.
- Distance to R_B = 30 cm (0.3 m) from A.
W2×0.2+W1×0.15−RB×0.3=0
Substituting the weights:
30N×0.2+20N×0.15−RB×0.3=0
Calculating the left side:
6+3−0.3RB=0
9=0.3RB
RB=90.3=30N(2)
Now, substitute RB back into equation (1):
RA+30N=50N
RA=50N−30N=20N(3)
- Reaction at edge A, RA=20N
- Reaction at edge B, RB=30N
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A metal bar 70cm long and 4.00kg in mass is supported on two knife edges placed 10cm from each end. A 6.00kg weight is suspended at 30cm from one end. Find the reactions at the knife edges. Assume the bar to be of uniform cross-section and homogeneous.
View SolutionA body of length 6 cm is placed 10cm from a concave mirror of focal length 20cm. Find the position, size, and nature of the image.
View Solution
Knowledge Check
A uniform rod of length 1m mass 4kg is supports on tow knife-edges placed10cm from each end. A 60N weight is suspended at 30cm from one end. The reactions at the knife edges is.
Aa. 60 N, 40 NBb. 75 N, 25 NCc. 65 N, 35 NDd. 55 N, 45 N
A 4 m long rod of negligible weight is supported at a point 125 cm from its one end and a load of 18 kgf is suspened at a point 60 cm from the support on the shorter arm.
(a) If a weight W is placed at a distance 250 cm from the support on the longer arm to balance the rod, find W.
(b) If a weight 5 kgf is kept to balance the rod, find its position.
(c) To which class of lever does it belong ?
View SolutionA block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
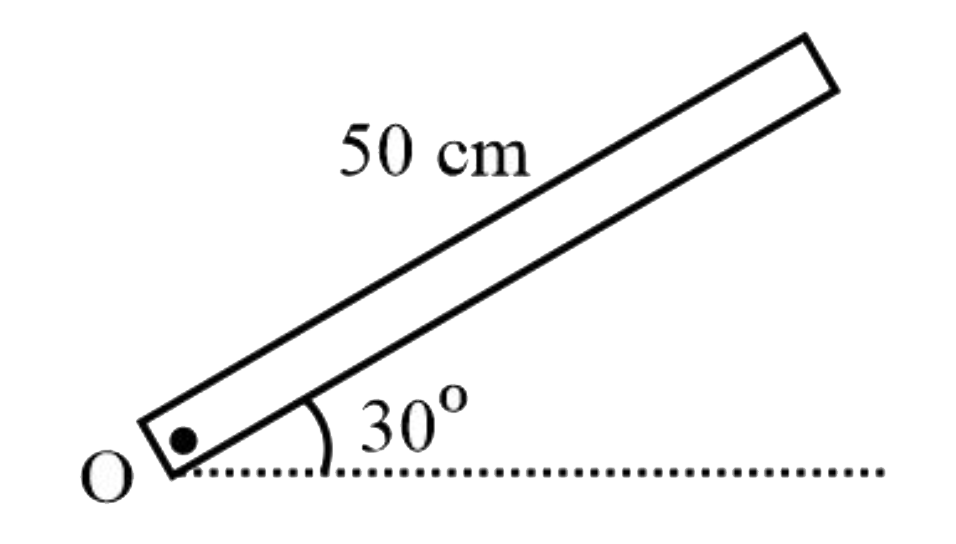
View SolutionA uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
View SolutionA ball of mass 1 kg is dropped from 20 m height on ground and it rebounds to height 5m. Find magnitude of change in momentum during its collision with the ground. (Take g=10m/s2)
View SolutionTwo cubes each of 10cm edge are joined end to end. Find the surface area of the resulting cuboid.
View SolutionIn a smooth hemispherical shell of radius R, a rod of mass (√3/2) kg is placed horizotally and is in equilibrium. The length of rod is R. Find the normal reaction at any end of the rod (in N). (Take g=10m/s2)
View SolutionA wire 2 m in length suspended vertically stretches by. 10 mm when mass of 10 kg is attached to the lower end. The elastic potential energy gain by the wire is (take g = 10m/s2)
View Solution
