The objects in the figure are constructed of uniform wire bent into the shape shown. Find the position of the position of the centre of mass of each shape.

(a) The centre of mass of each wire of length L will lie on its mid-point. Each rod will have same mass (say m) so, the centre of mass (C ) of the system will be at the mid-point of the line-segment joining C1 and C2. Hence OC is the bisector of the angle θ.
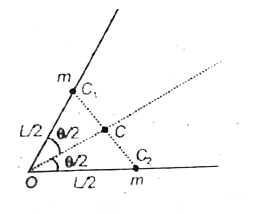
From the figure, clearly,
OC=L2cos.θ2
(b) Figure (b), shows C1,C2 and C3 as the positions of the centre of masses of the wires. C4 is the position of the centre of mass of the two vertical rods. Hence at C4, the mass 2m has been supposed to be placed.
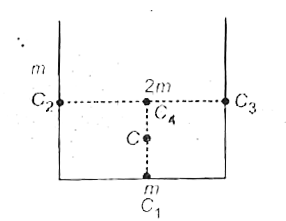
Now, C1C=2mm+2m(C1C4)=23.L2=L3
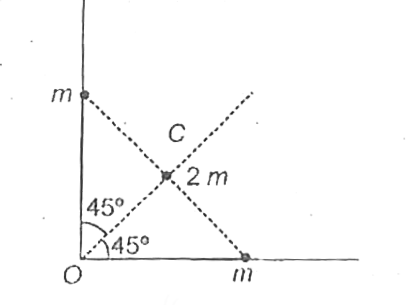
(c ) Putting θ=90∘ in (a) we get the position of c.m.
OC=L2cos45∘=L2√2
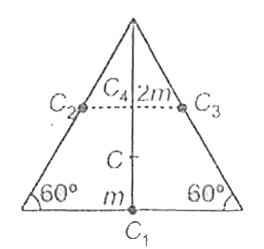
(d) The position of the centre of mass (C ) of the system is given by
C1C=2mm+2m(C1C4)
=23(L2sin60∘)
=L√3
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
Knowledge Check
Which of the following points is the likely position of the centre of mass of the system shown in Fig.
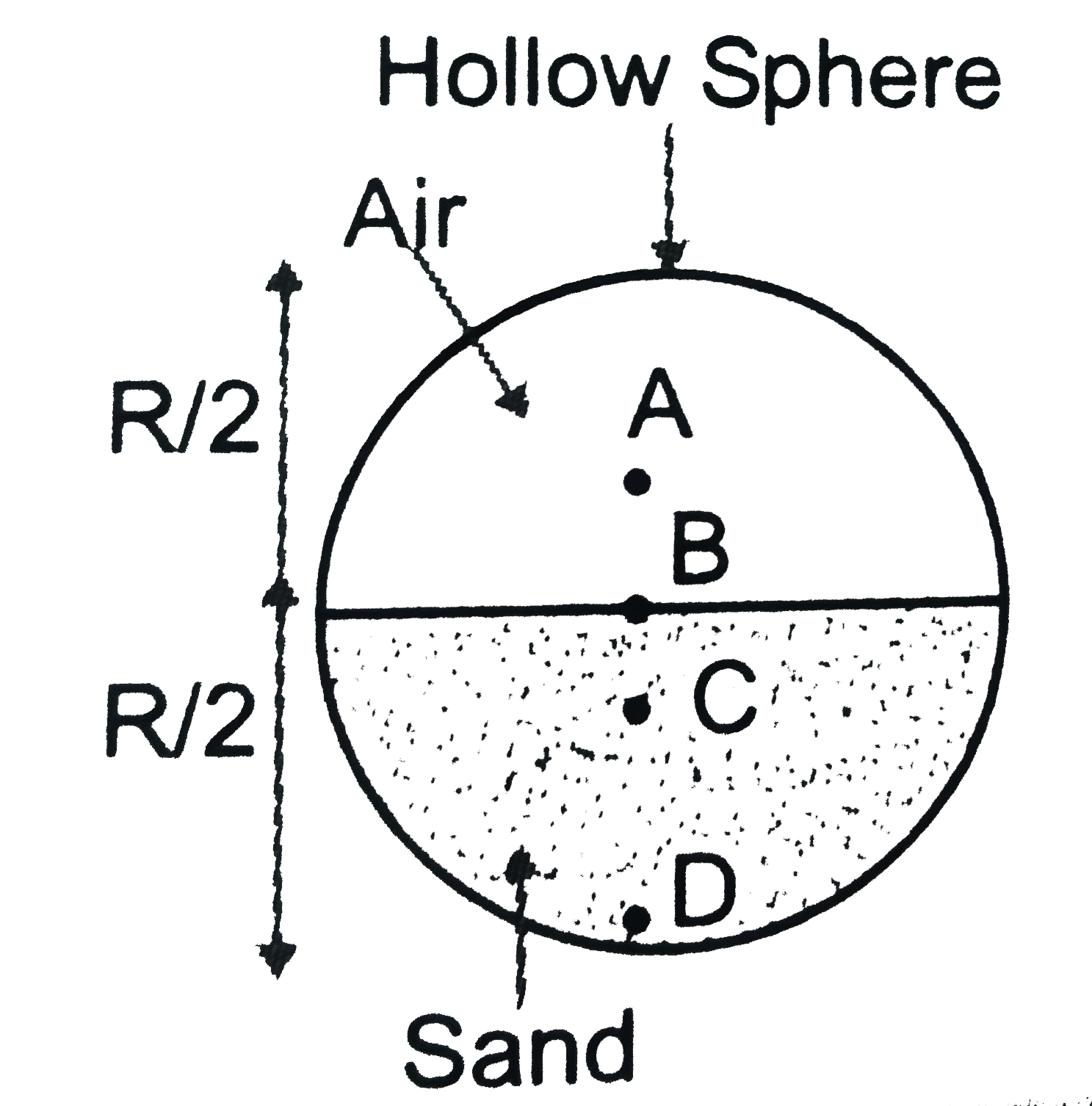 AABBCCDD
AABBCCDD
Find the position of centre of mass of the section shown in figure

View SolutionA thick uniform wire is bent into the shape of the letter “U” as shown. Which point indicates the location of the center of mass of this wire?
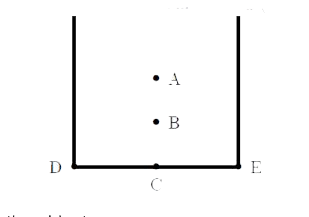
View SolutionWhich of the following points is the likely position of the centre of mass of the system shown in Fig.

View SolutionWhich of the following points is the likely position of the centre of mass of the system shown in Fig.

View SolutionWhich of the following points is the likely position of the centre of mass of the system shown in Fig.

View SolutionA uniform wire of length l is bent into the shape of 'V' as shown. The distance of its centre of mass from the vertex A is :-

View SolutionThe uniform solid sphere shown in the figure has a spherical hole in it. Find the position of its centre of mass.
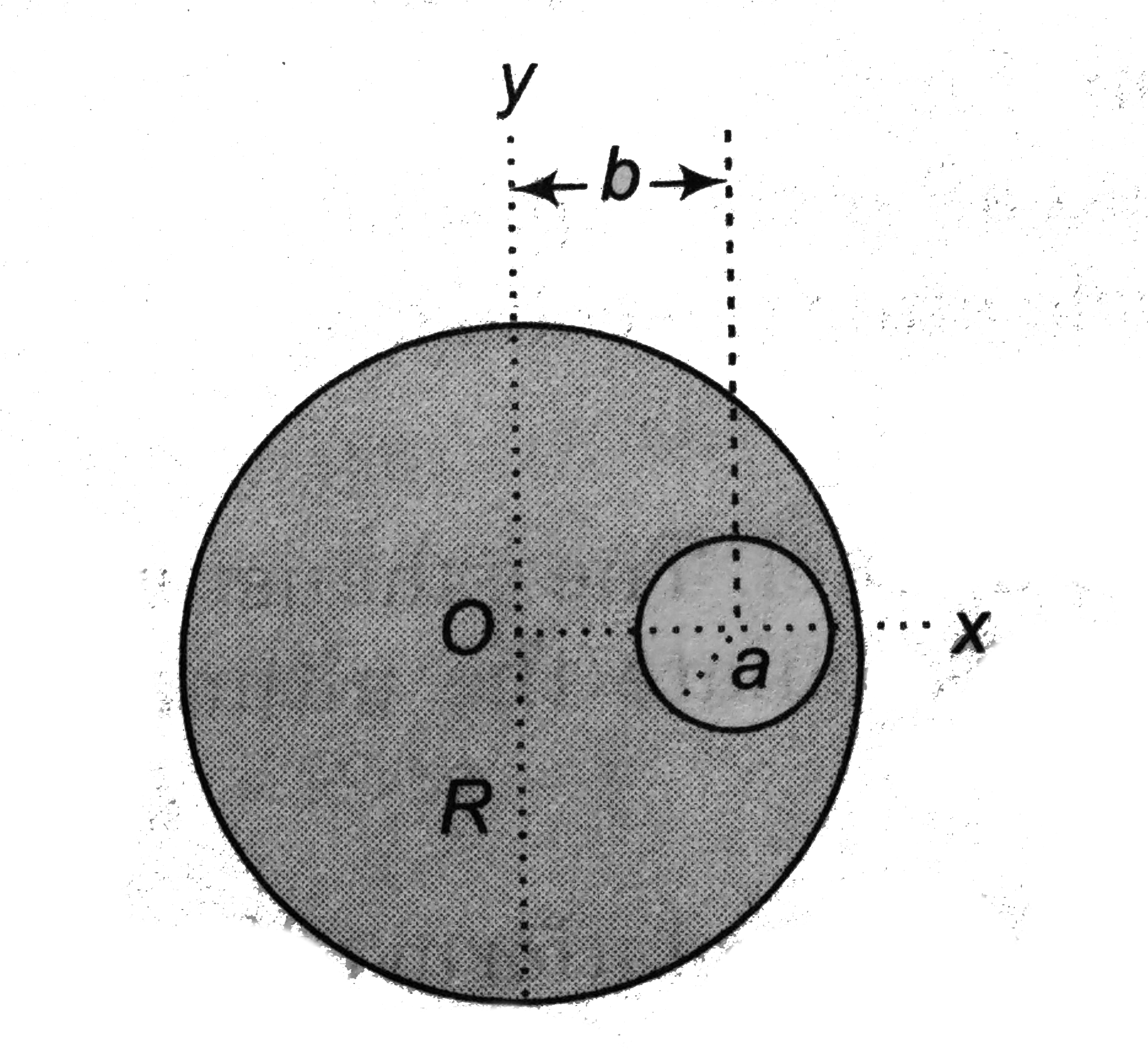
View Solution


 .
.