The linear density of a thin rod of length 1m lies as , where x is the distance from its one end. Find the distance of its center of mass from this end.
Let us consider a small length dx of the rod shown in the figure.
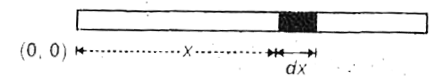
Its mass
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Illustration
Explore 4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - A) Objective Type Questions (One option is correct)
Explore 62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTE ENGLISHChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTE ENGLISHChapter:TEST 1Exercise:EXERCISE
Explore 21 Videos
Similar Questions
The liner density of a rod of length 2m varies as λ=(2+3x) kg/m, where x is distance from end A . The distance of a center of mass from the end B will be
_PHY_E05_180_Q02.png)
View SolutionThe density of a rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionThe linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
View SolutionThe density of a thin rod of length l varies with the distance x from one end as ρ=ρ0x2l2. Find the position of centre of mass of rod.
View SolutionIf linear density of a rod of length 3m varies as λ=2+x, them the position of the centre of gravity of the rod is
View SolutionThere is a rod of length l , its density varies with length as distance of λ=ax , where x is distance from left end. Find center of mass from left end.
View SolutionFind centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
View SolutionA heavy metallic rod of non-uniform mass distribution, is hanged vertically from a rigid support. The linear mass density varies as λ(x)=k×x where x is the distance measured along the length of rod, from its lower end. Find extension in rod due to its own weight.
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionIf the linear mass density of a rod of length 3 m (lying fromy=0 toy=3m) varies as λ=(2+y)kg/m,then position of the centre of mass of the rod from y=0 is nearly at
View Solution