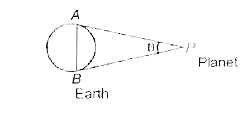
The parallax of a far off planet as measured from the two diametric extremes on the equator of the earth is 2.0 minute. If the radius of the earth is 6400 km, find the distance of the planet from the earth.
Angle of parallx θ = 2 minute
= 2×(160)2
⇒0=2×160×π180rad [∵1∘−π180rad]
θ=π5400rad
From parallax method
BP=ABθ
⇒BP=Diameter of earthθ
⇒BP=2×6400(π5400)km
⇒BP=2.2×107km
=2.2×1010m
Similar Questions
The parallax of a heavenly body measured from tow points diametrically opposite on equator of earth is 2.0 minute. If radius of earth is 6400 km, calculate distance of heavenly body.
View SolutionFind out the capacitance of the earth ? (Radius of the earth = 6400 km)
View SolutionThe radius of the Earth is 6400 km. If the height of an antenna is 500 m, then its range is
View SolutionWhat is the linear velocity of a person at equator of the earth due to its spinning motion? (Radius of the earth = 6400 km.)
View SolutionThe density of a newly discovered planet is twice that of earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth is R, the radius of the planet would be
View SolutionFind the depth at which the value of g becomes 25% of that at the surface of the earth. (Radius of the earth = 6400 km)
View SolutionFind the acceleration of a particle placed on the surface of the earth at the equator, due to the earth rotation. The radius of earth is 6400 km and time period of revolution of the earth about its axis is 24 h.
View SolutionWhat is the linear velocity of a body on the surface of the earth at the equator ? Given the radius of the earth is 6400 km . Period of rotation of the earth = 24 hours.
View SolutionFrom two diametrically opposite points A and B on earth, moon is observed. The angle θ subtended at the moon by the two directions of observation is 1∘541. If radius of earth is0.638×107 m, find the distance of the moon from the earth.
View SolutionAt what height above the surface of earth the value of "g" decreases by 2 % [ radius of the earth is 6400 km ]
View Solution
