For the following arrangement, find the equivalent capacitance between A and B
 .
.
Video Solution
Text Solution
Here, the 3μF,4μF and 5μF capacitors are in series.
∴Ceq=(13+14+15)−1=6012+20+15=6047μF
Now, 2μF and 6047 are in parallel , so we have
Ceq=C1+C2=15447μF
|
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A
44 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions
5 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Find the equivalent capacitance between C and B.
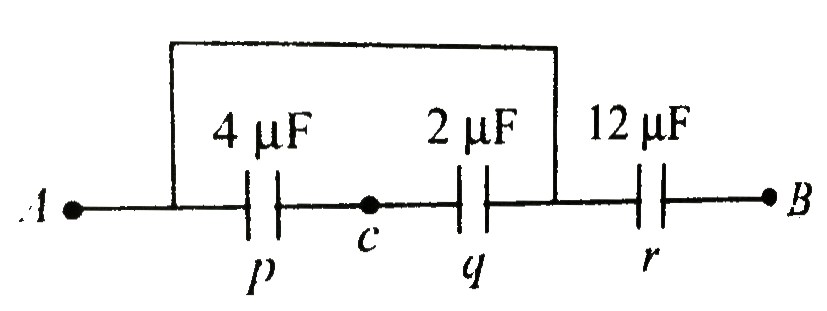
View SolutionThe equivalent capacitance between A and B is

View SolutionThe equivalent capacitance between A and B is
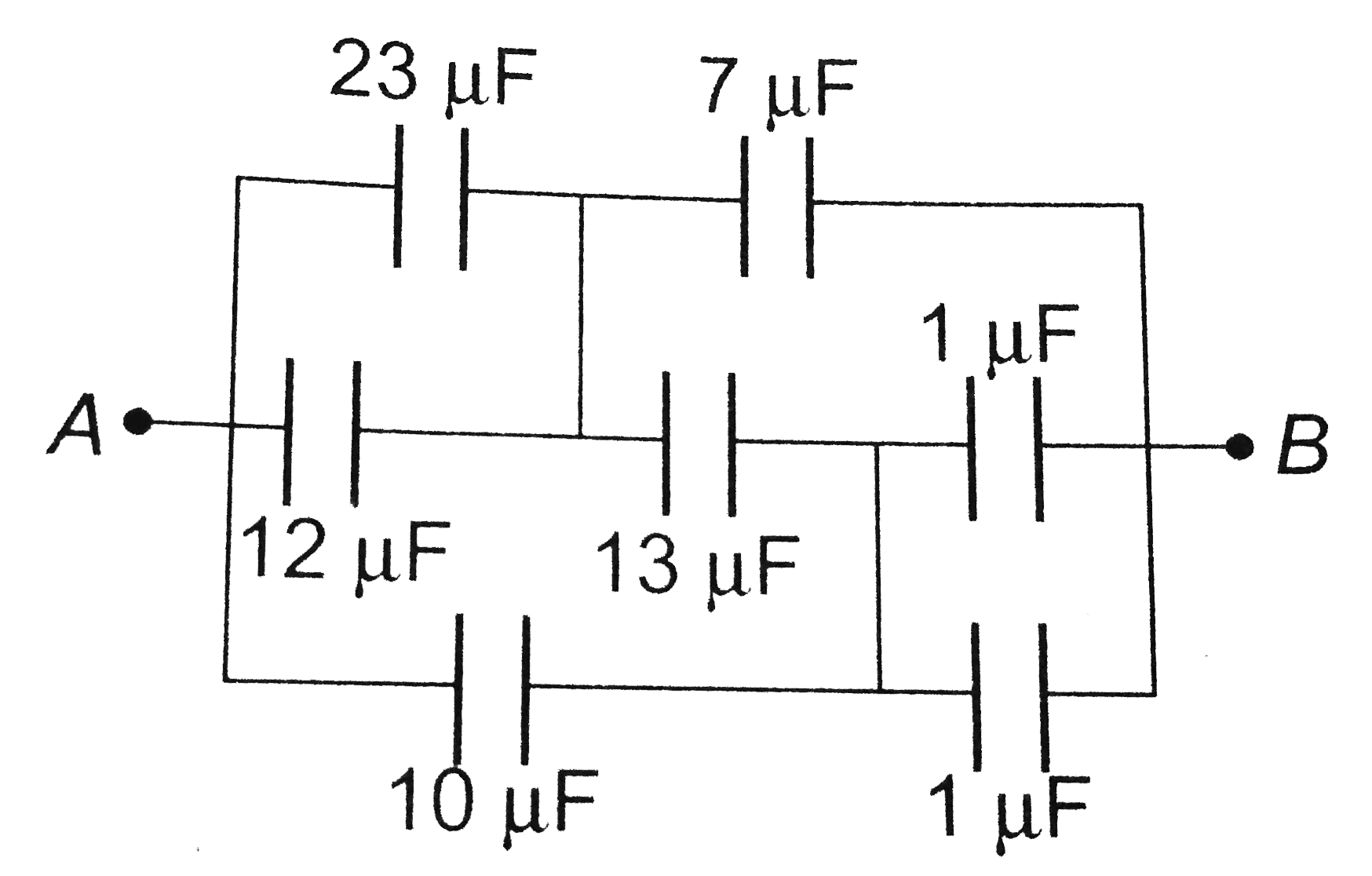
View SolutionEquivalent capacitance between A and B is
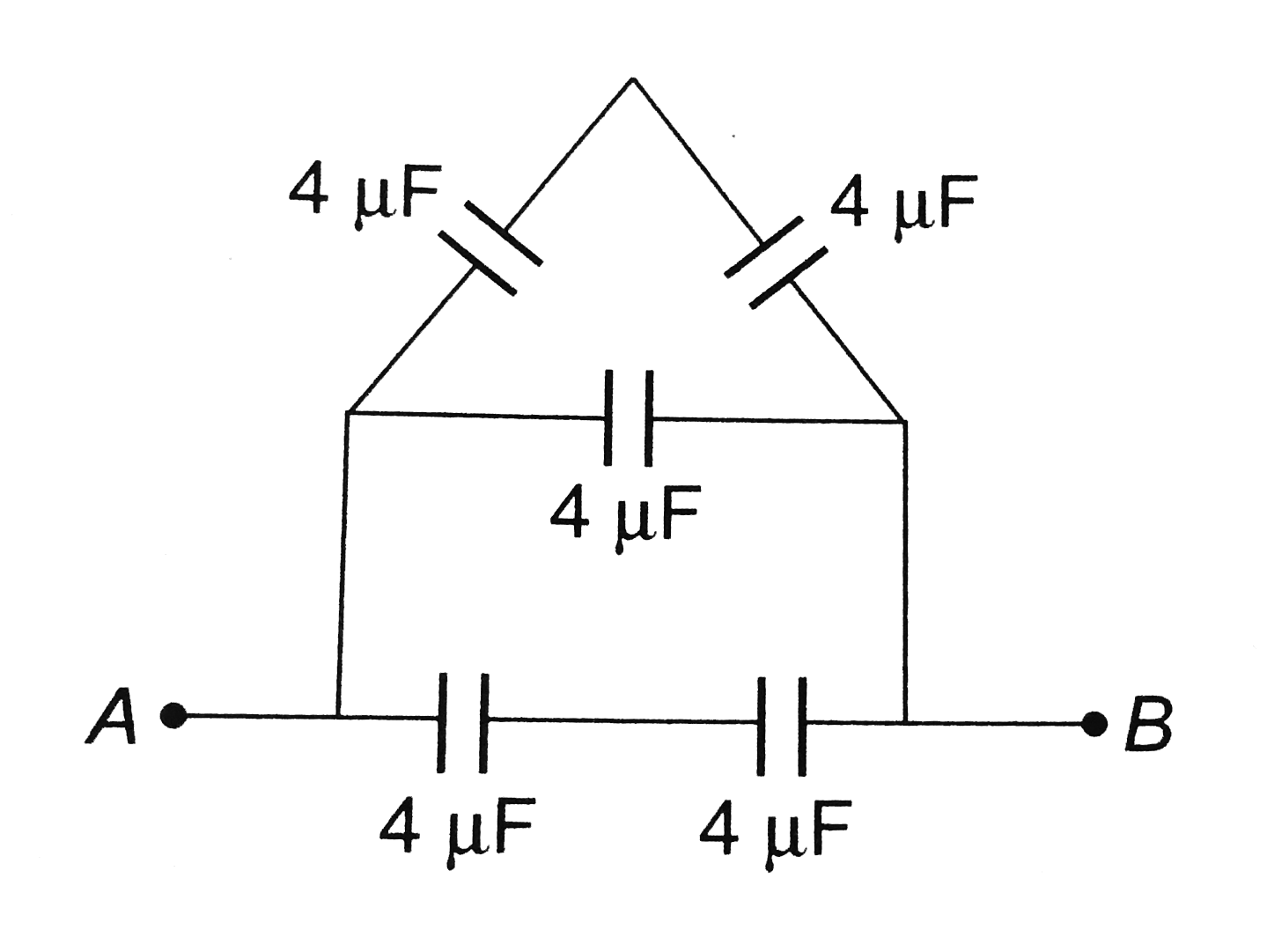
View SolutionFind out equivalent capacitance between A and B.

View SolutionEquivalent capacitance between A and B is:
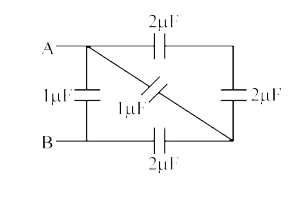
View SolutionFind equivalent capacitance between A and B
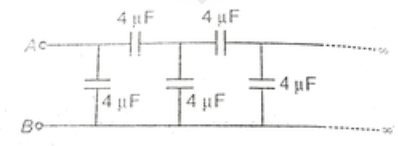
View SolutionFind the equivalent capacitance between point A and B .
View SolutionThe equivalent capacitance between A and B will be
View SolutionThe equivalent capacitance between X and Y is
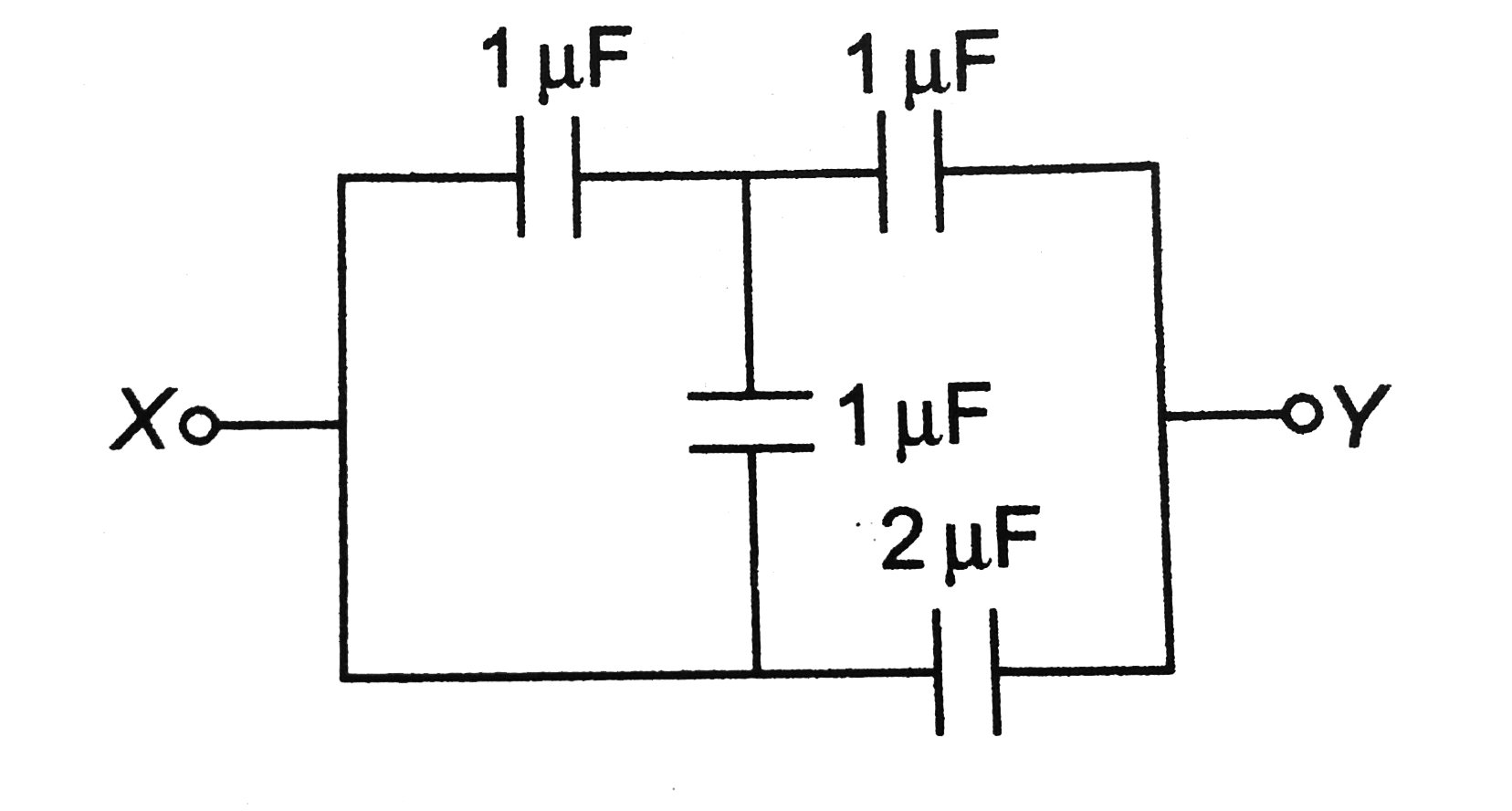
View Solution
