A particle of mass m and charge q is suspended from a point A with a silk thread of length l. Another particle of charge −q is fixes at a distance I from the point A such that point A and the charge -q lie in same horizontal plane. If at equilibrium , the thread makes angle 30∘ with vertical, find the mass m and tension in the thread . ( Take acceleration due to gravity as g).
To solve the problem, we need to analyze the forces acting on the charged particle of mass m and charge q suspended from point A. The particle is in equilibrium, making an angle of 30∘ with the vertical due to the electrostatic force exerted by the fixed charge −q.
1. Identify the Forces:
- The gravitational force acting downward: Fg=mg
- The tension in the thread: T
- The electrostatic force between the two charges: Fe
2. Draw a Free Body Diagram:
- The tension T can be resolved into two components:
- Vertical component: Tcos(30∘)
- Horizontal component: Tsin(30∘)
3. Set Up the Equilibrium Conditions:
- In the vertical direction (y-axis):
Tcos(30∘)=mg(1)
- In the horizontal direction (x-axis):
Tsin(30∘)=Fe(2)
4. Calculate the Electrostatic Force:
- The electrostatic force Fe between the charges q and −q is given by Coulomb's law:
Fe=14πϵ0q2r2
- Here, r is the horizontal distance between the two charges. Since the thread makes an angle of 30∘ with the vertical, we can express r in terms of l (length of the thread):
r=lsin(30∘)=l2
- Therefore, substituting for r:
Fe=14πϵ0q2(l2)2=4q2πϵ0l2(3)
5. Substituting Fe into Equation (2):
Tsin(30∘)=4q2πϵ0l2
Since sin(30∘)=12:
T⋅12=4q2πϵ0l2
Thus,
T=8q2πϵ0l2(4)
6. Substituting T into Equation (1):
8q2πϵ0l2cos(30∘)=mg
Since cos(30∘)=√32:
8q2πϵ0l2⋅√32=mg
Simplifying gives:
mg=4√3q2πϵ0l2(5)
7. Finding the Mass m:
m=4√3q2gπϵ0l2(6)
Final Results:
- The mass m of the particle is:
m=4√3q2gπϵ0l2
- The tension T in the thread is:
T=8q2πϵ0l2
- The gravitational force acting downward: Fg=mg
- The tension in the thread: T
- The electrostatic force between the two charges: Fe
- The tension T can be resolved into two components:
- Vertical component: Tcos(30∘)
- Horizontal component: Tsin(30∘)
- In the vertical direction (y-axis):
Tcos(30∘)=mg(1)
- In the horizontal direction (x-axis):
Tsin(30∘)=Fe(2)
- The electrostatic force Fe between the charges q and −q is given by Coulomb's law:
Fe=14πϵ0q2r2
- Here, r is the horizontal distance between the two charges. Since the thread makes an angle of 30∘ with the vertical, we can express r in terms of l (length of the thread):
r=lsin(30∘)=l2
- Therefore, substituting for r:
Fe=14πϵ0q2(l2)2=4q2πϵ0l2(3)
Tsin(30∘)=4q2πϵ0l2
Since sin(30∘)=12:
T⋅12=4q2πϵ0l2
Thus,
T=8q2πϵ0l2(4)
8q2πϵ0l2cos(30∘)=mg
Since cos(30∘)=√32:
8q2πϵ0l2⋅√32=mg
Simplifying gives:
mg=4√3q2πϵ0l2(5)
m=4√3q2gπϵ0l2(6)
- The mass m of the particle is:
m=4√3q2gπϵ0l2
- The tension T in the thread is:
T=8q2πϵ0l2
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:TRY YOURSELF
Explore 33 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:ASSIGNMENT(SECTION-A) Objective Type Question
Explore 45 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
Explore 15 Videos
Similar Questions
The charges +4q and +q are at a distance 3m apart. At what point between the charges, a third charge +q must be placed to keep it in equilibrium ?
View SolutionTwo fixed charges +4q and +q are at a distance 3 m apart. At what point between the charge, a third charge +q must be placed to keep it in equilibrium ?
View Solution
Knowledge Check
A point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
Adirected perpendicular to the plane and away from the plane.Bdirected perpendicular to the plane but towards the plane.Cdirected radially away from the point charge.Ddirected radially towards the point charge.
A point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View SolutionA point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
View SolutionA particle of mass m and positive charge q is released from point A. Its speed is found to be v when it passes through a point B. which of the two points is at higher potential ? What is the potential difference between the points?
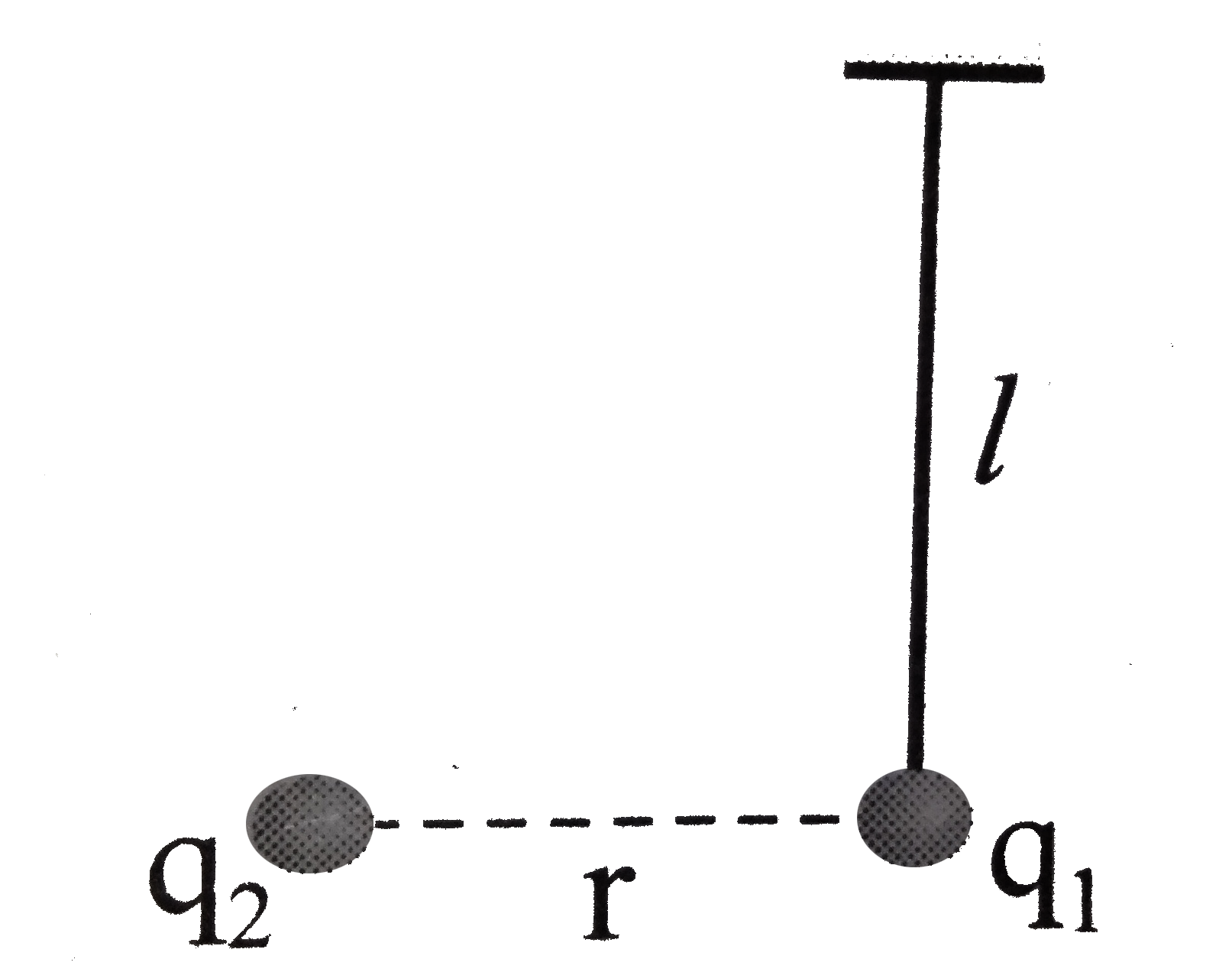
View SolutionAn isolated charge q1 of mass m is suspended freely by a thread of length l. Another charge q2 is brought near it (r>>l). When q1 is in equilibrium tension in thread will be
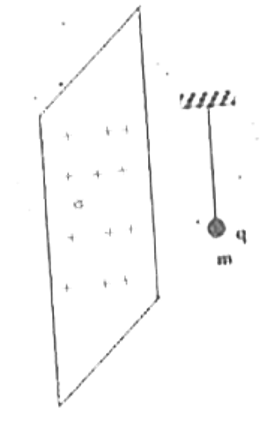
View SolutionA small charged particle of mass m and charge q is suspended by an insulated thread in front of a very large conducting charged sheet of uniform surface density of charge σ. The angle made by the thread with the vertical in equilibrium is
View Solution