A spherical vessel of radius r = 5 cm contains hydrogen (H2) at a temperature T=300 K and pressurep=105 Pa. How many molecules collide on the vessel in 1 s ?
To determine how many molecules collide with the walls of a spherical vessel containing hydrogen gas in one second, we can follow these steps:
Step 1: Calculate the RMS velocity of hydrogen molecules
The formula for the root mean square (RMS) velocity vrms is given by:
vrms=√3RTM
Where:
- R is the universal gas constant =8.314J/(mol K)
- T is the temperature in Kelvin =300K
- M is the molar mass of hydrogen in kg/mol. Since the molar mass of H2 is 2g/mol, we convert it to kg:
M=2×10−3kg/mol
Substituting the values:
vrms=√3×8.314×3002×10−3
Calculating this gives:
vrms=√249420.002=√12471000≈3537.5m/s
Step 2: Calculate the mean free path λ
The mean free path λ can be calculated using the formula:
λ=RT√2πσ2NAP
Where:
- σ is the collision cross-section for hydrogen, which is given as 289pm=289×10−12m
- NA is Avogadro's number =6.022×1023molecules/mol
- P is the pressure =105Pa
Substituting the values:
λ=8.314×300√2π(289×10−12)2(6.022×1023)(105)
Calculating this gives:
λ≈6.72×10−8m
Step 3: Calculate the collision frequency
The collision frequency Z (the number of molecules colliding with the walls in one second) can be calculated using:
Z=vrmsλ
Substituting the values we calculated:
Z=3537.56.72×10−8≈5.26×1014collisions/s
Step 4: Calculate the number of molecules in the vessel
To find the number of molecules N in the vessel, we can use the ideal gas law:
PV=nRT
Where n is the number of moles, and V is the volume of the spherical vessel:
V=43πr3
Substituting r=0.05m:
V=43π(0.05)3≈5.24×10−4m3
Now, substituting into the ideal gas law:
n=PVRT=(105)(5.24×10−4)(8.314)(300)≈0.021mol
Calculating the number of molecules:
N=n×NA≈0.021×6.022×1023≈1.26×1022molecules
Final Calculation of Collisions per Second
Now we can calculate the number of collisions per second:
Number of collisions per second=Z×N≈5.26×1014×1.26×1022≈6.63×1036collisions/s
Conclusion
Therefore, the number of molecules colliding with the vessel in one second is approximately 6.63×1036.
---
- R is the universal gas constant =8.314J/(mol K)
- T is the temperature in Kelvin =300K
- M is the molar mass of hydrogen in kg/mol. Since the molar mass of H2 is 2g/mol, we convert it to kg:
- σ is the collision cross-section for hydrogen, which is given as 289pm=289×10−12m
- NA is Avogadro's number =6.022×1023molecules/mol
- P is the pressure =105Pa
Topper's Solved these Questions
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assignment (Section-J) (Aaksh challengers Questions)
3 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (TRY YOURSELF)
40 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assignment (Section-H) (Multiple True-false Type questions)
3 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
Similar Questions
A closed vessel of volume 0.2m3 contain hydrogen gas at temperature 300K and pressure 105Pa. Then the heat required to raise temperature to 600K is:(molar heat capacity of hydrogen at constant volume is 5cal/mol−K)
View SolutionSolve
A vessel contains X number of molecules of hydrogen gas at a certain temperature and pressure. How many molecules of nitrogen gas would be present in the same vessel under the same conditions of temperature and pressure ?
View Solution
Knowledge Check
A vessel contains a mixtrue consisting of m1=7g of nitrogen M1=28andm2=11g of carbon dioxide (M244) at temperatureT=300K and pressure p0=1 atm. Find the density of the mixture.
A1.446 g per litreB2.567 g per litreC3.752 g per litreD4.572 g per litre
A vessel contains X number of molecule of hydrogen gas at a certain temperature and pressure. How many molecules of oxygen will be present in a vessel of same volume under the same conditions of temperature and pressure? Name the law to justify your answer.
View SolutionA vessel of volume 0.2m3 contains hydrogen gas at temperature 300 K and pressure 1 bar. Find the heat required to raise the temperature to 400 K. The molar heat capacity of hydrogen at constant volume is 5cal/molK.
View SolutionA vessel of capacity 600cm3 contains hydrogen gas at a pressure of 304 cm Hg. What will be the pressure of hydrogen gas, when the vessel is connected to another vessel of 300cm3 capacity ?
View SolutionThree closed rigid vessels, A, B and C, which initially contain three different gases at different temperatures are connected by tube of negligible volume, without any energy transfer with surroundings. The vessel A contain 2 mole Ne gas, at 300 K, vessel 'B' contain 2 mole SO2 gas at 400 K and vessel 'C' contain 3 mole CO2 gas at temperature 500 K. What is the final pressure (in atm) attained by gases when all valves of connecting three vessels are opened and additional 15.6 kcal hear supplied to vessels through valve. The volume of A, B and C vessel is 2, 2 and 3 litre respectively
Given :R =2 calorie/mol-K,Cv(Ne)=3/2R,Cv(CO)=5/2RandCv(SO2)=3R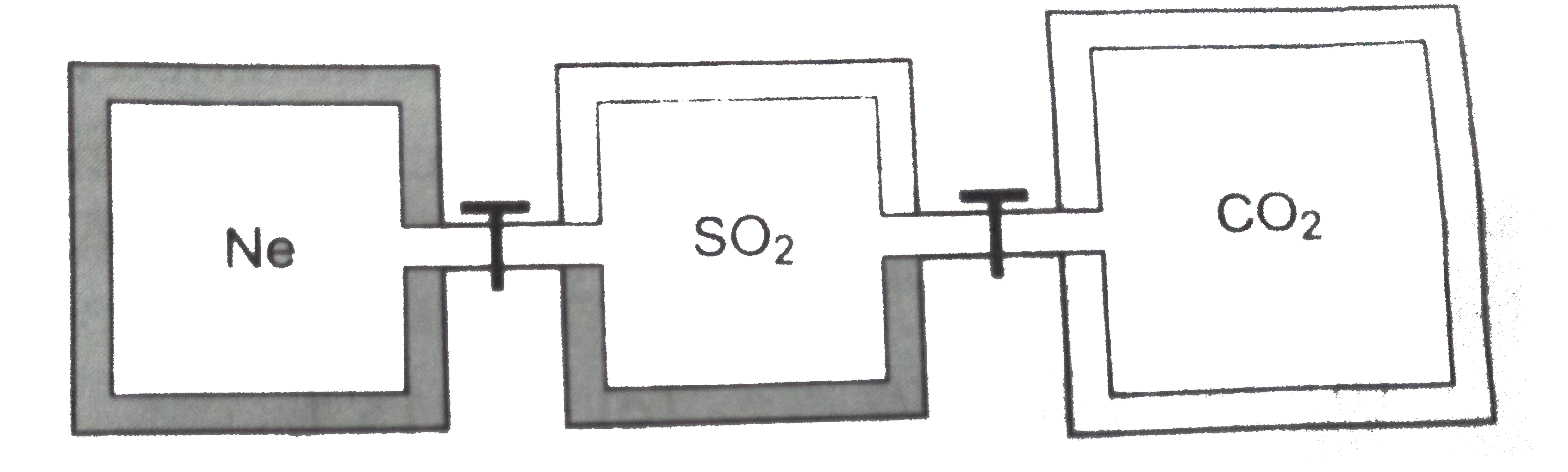
View SolutionA vessel of capacity 600 cm contains hydrogen A vessel of capacity 600 cm^3 contains hydrogen be the pressure of hydrogen gas, when the vessel is connected to another vessel of 300 cm^3
View SolutionA closed vessel A having volume V contains N2 at pressure P and temperature T. another closed vessel B having the same volume V contains. He at the same pressure P. but temperature 2T. The ratio of masses of N2 and He in the vesses A and B is
View SolutionVessel A contains an ideal gas at a pressure 5×105 Pa and is connected with a heat source which maintains its temperature at 300K. Another vessel B which has four time greater inner volume contains the same gas at a pressure 105 Pa and is connected to a heat source which maintains its temperature at 400K. What will be the pressure of entire system if two vessels are connected by a narrow tube tap:-
View Solution
