A cubical box containing 2 mole of He gas moves with constant speed u on a smooth horizontal surface. If the box suddenly stops, then determine the change in temperature of the gas by assuming mass of box to be negligible.
To determine the change in temperature of the helium gas when the cubical box suddenly stops, we can follow these steps:
Step 1: Understand the Energy Conservation Principle
When the box stops, the kinetic energy of the box and the gas inside it is converted into internal energy of the gas, resulting in an increase in temperature. According to the principle of conservation of energy:
ΔU=−ΔK
where ΔU is the change in internal energy and ΔK is the change in kinetic energy.
Step 2: Calculate the Change in Kinetic Energy
The kinetic energy (K) of the system when it is moving with speed u is given by:
K=12mu2
Since the mass of the box is negligible, we only consider the mass of the gas. For 2 moles of helium gas, the mass can be calculated as follows:
- The molar mass of helium (He) is approximately 4 g/mol.
- Therefore, the mass of 2 moles of helium is:
m=2×4g=8g=8×10−3kg
Now, substituting this into the kinetic energy formula:
ΔK=−12(8×10−3)u2
Step 3: Relate Change in Internal Energy to Temperature Change
The change in internal energy (ΔU) for an ideal gas is given by:
ΔU=nCVΔT
where n is the number of moles, CV is the molar specific heat at constant volume, and ΔT is the change in temperature.
For a monoatomic gas like helium, the molar specific heat at constant volume is:
CV=32R
where R is the universal gas constant, approximately 8.314J/(mol K).
Step 4: Substitute Values into the Equation
Now substituting the values:
ΔU=nCVΔT=2×32RΔT=3RΔT
Equating the change in internal energy to the negative change in kinetic energy:
3RΔT=−(−12(8×10−3)u2)
This simplifies to:
3RΔT=12(8×10−3)u2
Step 5: Solve for ΔT
Now, rearranging to find ΔT:
ΔT=(8×10−3)u26R
Substituting R=8.314J/(mol K):
ΔT=(8×10−3)u26×8.314
Calculating this gives:
ΔT=8×10−3u249.884≈1.6×10−4u2K
Final Answer
The change in temperature of the gas is:
ΔT≈1.6×10−4u2K
---
When the box stops, the kinetic energy of the box and the gas inside it is converted into internal energy of the gas, resulting in an increase in temperature. According to the principle of conservation of energy:
ΔU=−ΔK
where ΔU is the change in internal energy and ΔK is the change in kinetic energy.
The kinetic energy (K) of the system when it is moving with speed u is given by:
K=12mu2
Since the mass of the box is negligible, we only consider the mass of the gas. For 2 moles of helium gas, the mass can be calculated as follows:
- The molar mass of helium (He) is approximately 4 g/mol.
- Therefore, the mass of 2 moles of helium is:
m=2×4g=8g=8×10−3kg
Now, substituting this into the kinetic energy formula:
ΔK=−12(8×10−3)u2
The change in internal energy (ΔU) for an ideal gas is given by:
ΔU=nCVΔT
where n is the number of moles, CV is the molar specific heat at constant volume, and ΔT is the change in temperature.
CV=32R
where R is the universal gas constant, approximately 8.314J/(mol K).
Now substituting the values:
ΔU=nCVΔT=2×32RΔT=3RΔT
Equating the change in internal energy to the negative change in kinetic energy:
3RΔT=−(−12(8×10−3)u2)
This simplifies to:
3RΔT=12(8×10−3)u2
Now, rearranging to find ΔT:
ΔT=(8×10−3)u26R
Substituting R=8.314J/(mol K):
ΔT=(8×10−3)u26×8.314
Calculating this gives:
ΔT=8×10−3u249.884≈1.6×10−4u2K
The change in temperature of the gas is:
ΔT≈1.6×10−4u2K
Topper's Solved these Questions
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Try Yourself
43 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assignment (Section-A) Objective type questions (One option is correct)
49 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
Similar Questions
A box of negligible mass containing 2 moles of an ideal gas of molar mass M and adiabatic exponent γ moves with constant speed v on a smooth horizontal surface. If the box suddenly stops, then change in temperature of gas will be :
View SolutionAn insulated container containing monoatomic gas of molar mass m is moving with a velocity V0. If the container is suddenly stopped , find the change in temperature .
View Solution
Knowledge Check
An insulated container containing monoatomic gas of molar mass m is moving with a velocity V0. If the container is suddenly stopped , find the change in temperature .
Amv202RBmv(0)23RCRmv20D3mv202RAn insulated container containing monoatomic gas of molar mass m is moving with a velocity V0. If the container is suddenly stopped , find the change in temperature .
Amv202RBmv203RC3mv202RD12mv20R
An insulated box containing a monoatomic gas of molar mass (M) moving with a speed v0 is suddenly stopped. Find the increment is gas temperature as a result of stopping the box.
View SolutionAn insulated box containing a monoatomic gas of molar mass (M) moving with a speed v0 is suddenly stopped. Find the increment is gas temperature as a result of stopping the box.
View SolutionA diatomic gas of molecular mass 40 g/mol is filled in rigid container at temperature 30∘C. It is moving with velocity 200 m/s. If its is suddenly stopped, the rise in the temperature of the gas is
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is
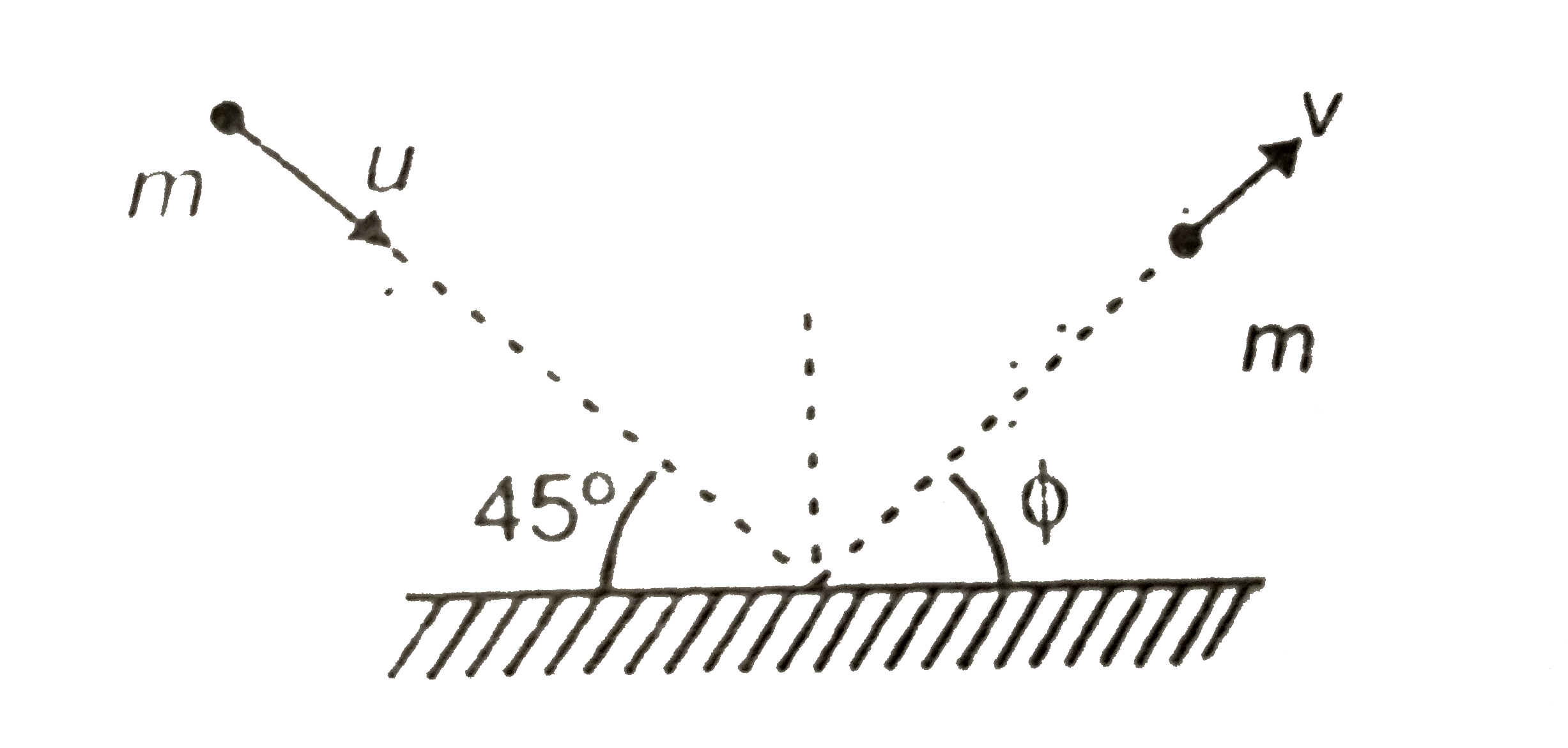
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is

View Solution
