A particle of mass m is whirled in horizontal circle with the help of two threads of length l each as shown in figure . Angular velocity equals ω, then
T1 equals
mg√3+mω2l2
mg√3+mω2l2
mω2l2
mg√3
The correct Answer is:A
To solve the problem of finding the tension T1 in the scenario where a particle of mass m is whirled in a horizontal circle using two threads of length l, we can follow these steps:
Step 1: Understand the Geometry
The particle is at a height and is moving in a horizontal circle. The threads make an angle with the vertical. For each thread, the vertical component of the tension must balance the weight of the mass, and the horizontal component provides the necessary centripetal force.
Step 2: Determine the Geometry of the Setup
From the geometry, we have:
- The angle made by the threads with the vertical is 30∘.
- The horizontal distance D from the vertical axis to the mass can be calculated using the sine function:
D=lsin(30∘)=l⋅12=l2
Step 3: Write the Forces in the Vertical Direction
For the vertical forces, we can write:
T1cos(30∘)+T2cos(30∘)=mg
Using cos(30∘)=√32, this becomes:
T1⋅√32+T2⋅√32=mg
Dividing through by √32:
T1+T2=2mg√3(Equation 1)
Step 4: Write the Forces in the Horizontal Direction
For the horizontal forces, the net centripetal force is provided by the horizontal components of the tensions:
T1sin(30∘)−T2sin(30∘)=mv2D
Substituting sin(30∘)=12:
12(T1−T2)=mv2D
Substituting D=l2 gives:
12(T1−T2)=mv2l2=2mv2l
Multiplying through by 2:
T1−T2=4mv2l(Equation 2)
Step 5: Solve the Equations
Now we have two equations:
1. T1+T2=2mg√3
2. T1−T2=4mv2l
Adding these two equations:
2T1=2mg√3+4mv2l
Thus,
T1=mg√3+2mv2l
Step 6: Relate Linear Velocity to Angular Velocity
The linear velocity v can be related to the angular velocity ω using the formula v=ωD:
v=ω⋅l2
Substituting this into the equation for T1:
T1=mg√3+2m(ω⋅l2)2l
This simplifies to:
T1=mg√3+mω2l2
Final Result
Thus, the tension T1 is given by:
T1=mg√3+mω2l2
The particle is at a height and is moving in a horizontal circle. The threads make an angle with the vertical. For each thread, the vertical component of the tension must balance the weight of the mass, and the horizontal component provides the necessary centripetal force.
From the geometry, we have:
- The angle made by the threads with the vertical is 30∘.
- The horizontal distance D from the vertical axis to the mass can be calculated using the sine function:
D=lsin(30∘)=l⋅12=l2
For the vertical forces, we can write:
T1cos(30∘)+T2cos(30∘)=mg
Using cos(30∘)=√32, this becomes:
T1⋅√32+T2⋅√32=mg
Dividing through by √32:
T1+T2=2mg√3(Equation 1)
For the horizontal forces, the net centripetal force is provided by the horizontal components of the tensions:
T1sin(30∘)−T2sin(30∘)=mv2D
Substituting sin(30∘)=12:
12(T1−T2)=mv2D
Substituting D=l2 gives:
12(T1−T2)=mv2l2=2mv2l
Multiplying through by 2:
T1−T2=4mv2l(Equation 2)
Now we have two equations:
1. T1+T2=2mg√3
2. T1−T2=4mv2l
2T1=2mg√3+4mv2l
Thus,
T1=mg√3+2mv2l
The linear velocity v can be related to the angular velocity ω using the formula v=ωD:
v=ω⋅l2
Substituting this into the equation for T1:
T1=mg√3+2m(ω⋅l2)2l
This simplifies to:
T1=mg√3+mω2l2
Thus, the tension T1 is given by:
T1=mg√3+mω2l2
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:ASSIGNMENT ( SECTION -C) objective type questions (More than one options are correct)
Explore 21 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question
Explore 1 Video
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:ASSIGNMENT ( SECTION -A)
Explore 50 Videos
- KINETIC THEORYBook:AAKASH INSTITUTE ENGLISHChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
Similar Questions
A particle of mass m is doing horizontal circular motion with the help of a string (conical pendulum) as shown in the figure. If speed of the particle is constant then,
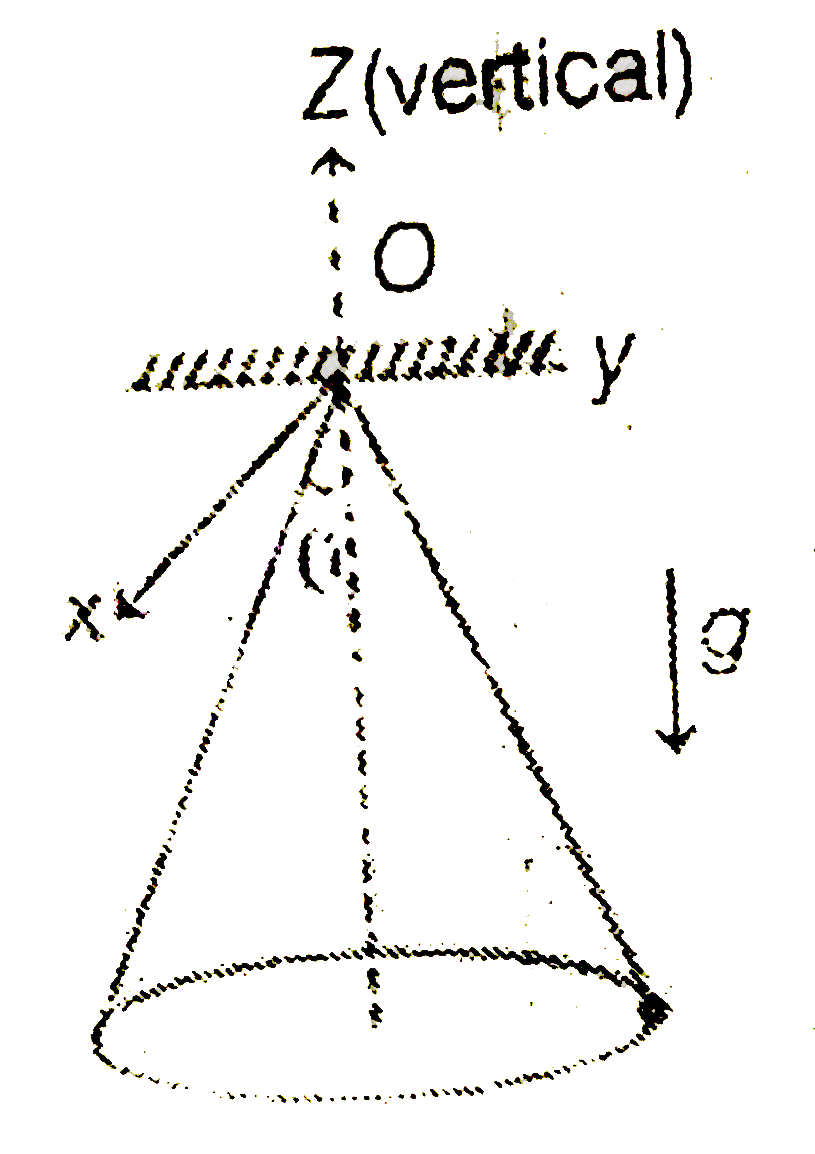
View SolutionA uniform rod PQ of mass m and length t rotates with an angular velocity a while its center moves with linear velocity v=2ω⋅f3 on a smooth horizontal surface If the end Q of the rod is suddenly gets stuck at the moment as shown in the figure then angular velocity of the rod will be
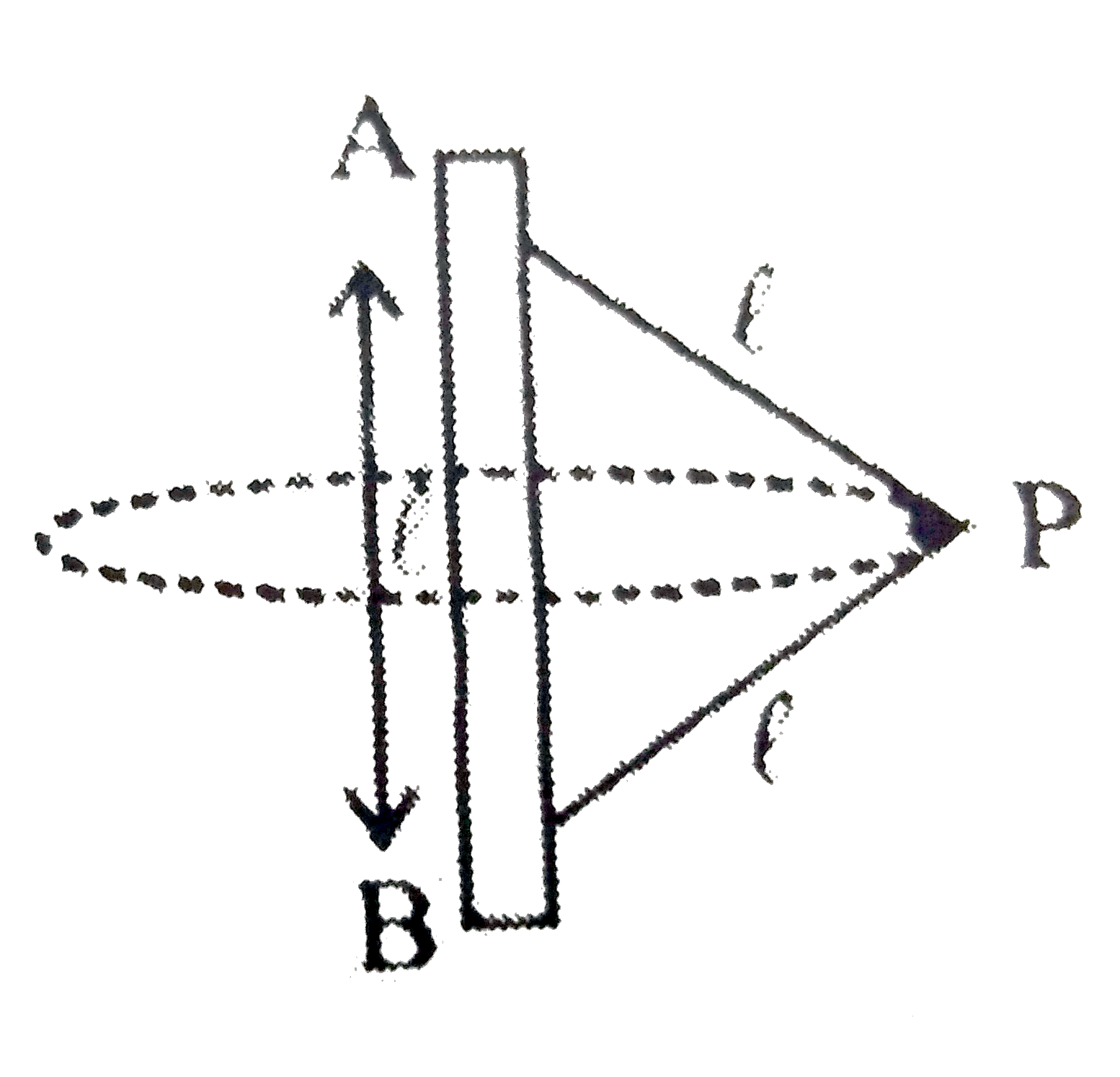
View SolutionA particle P of mass m is attached to a vertical axis by two strings AP and BP of length l each. The separation AB=l. P rotates around the axis with an angular velocity ω. The tensions in the two strings are T1andT2
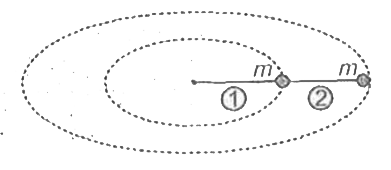
View SolutionTwo particles each of mass m are moving in horizontal circle with same angular speed. If both string are of same length then the ratio of tension in string T1T2 is
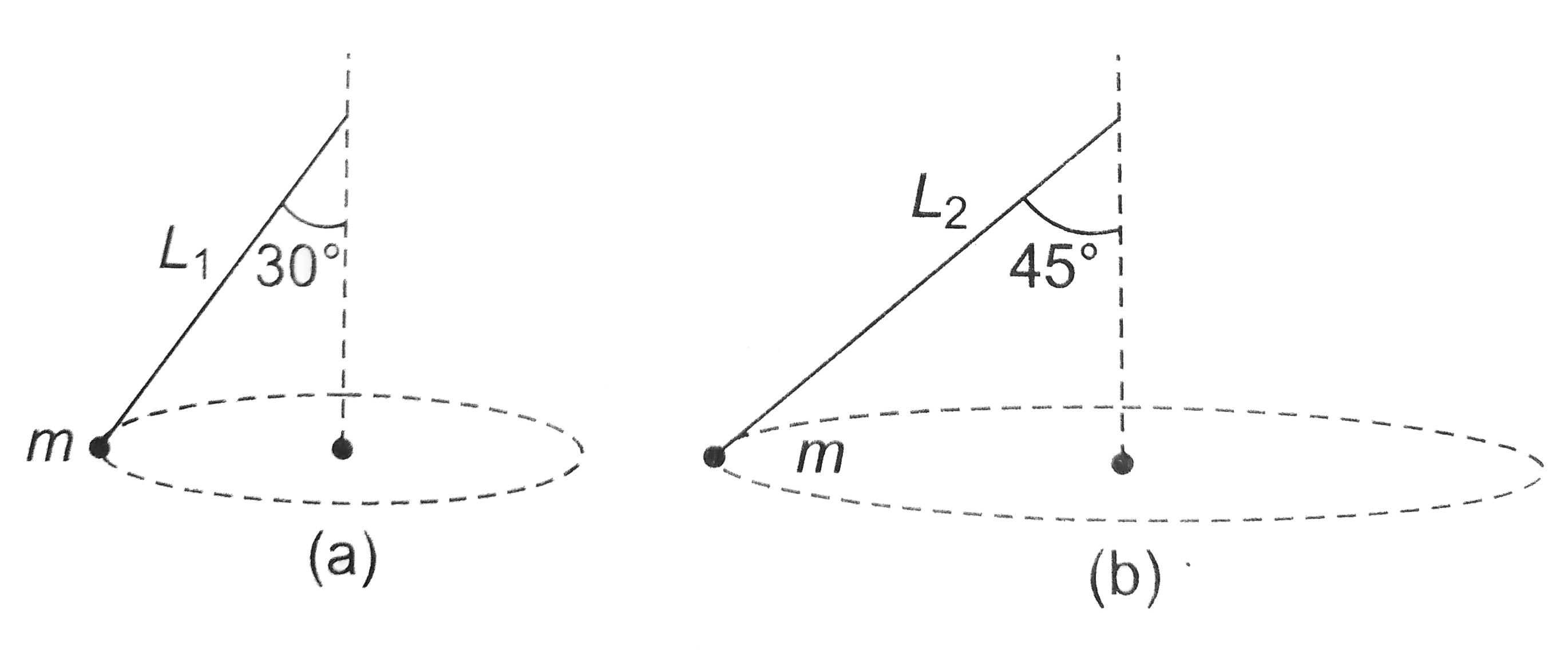
View SolutionTwo partical tied to different strings are whirled in a horizontal circle as shown in figure. The ratio of lengths of the string so that they complete their circular path with equal time period is:
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O. Match the following columns.
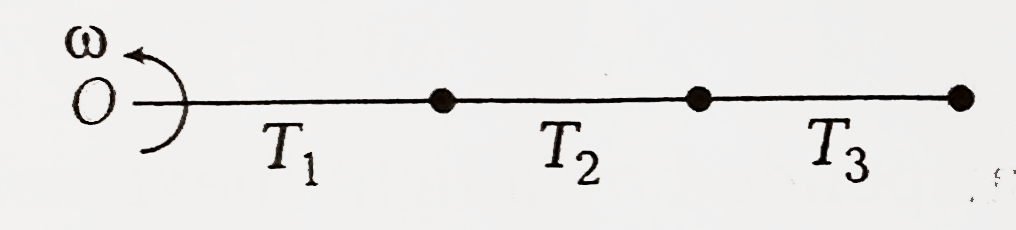
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O.find the tensions .
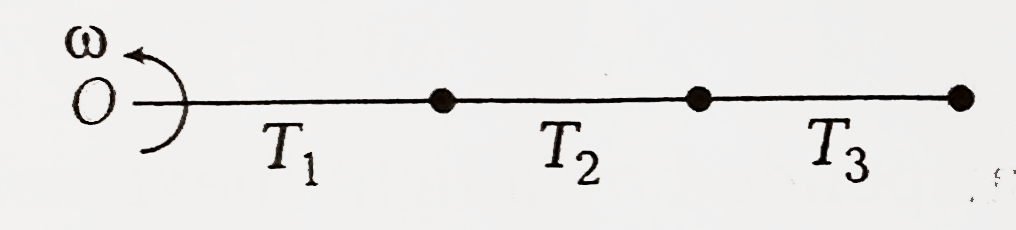
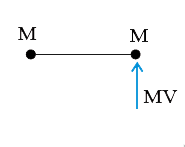
View SolutionTwo particles each of mass M are connected by a massless rod. The rod is lying on the smooth horizontal surface. If one of the particle is given an impulse MV as shown in the figure then angular velocity of the system would be:
View SolutionFour particles of equal mass are moving round a circle of radius r due to their mutual gravitational attraction . Find the angular velocity of each particle .
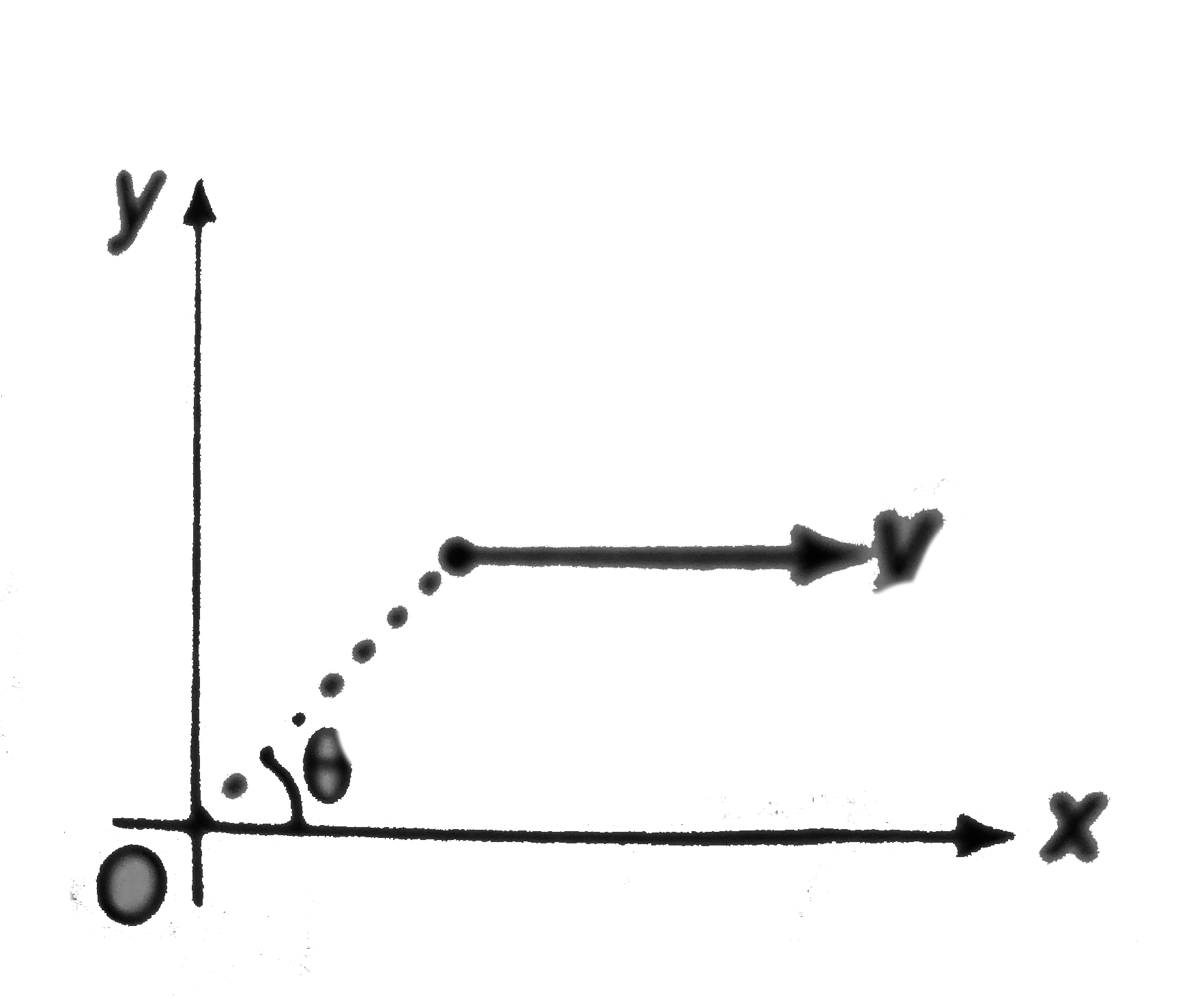
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O
View Solution

