A ray of light with wavelength 5000 nm travelling from a medium with refractive index (32) suffers partial reflection and refraction in a medium of refractive index (43). Find wavelength of reflected and refracted ray.
To solve the problem, we need to find the wavelengths of the reflected and refracted rays when a ray of light with a wavelength of 5000 nm travels from a medium with a refractive index of 32 to a medium with a refractive index of 43.
1. Identify Given Values:
- Wavelength of incident light, λ=5000nm
- Refractive index of the first medium, n1=32
- Refractive index of the second medium, n2=43
2. Determine Wavelength of the Reflected Ray:
- The wavelength of the reflected ray remains the same as that of the incident ray because reflection does not change the wavelength.
- Therefore, the wavelength of the reflected ray, λr=5000nm.
3. Calculate the Relative Refractive Index:
- The relative refractive index μ can be calculated using the formula:
μ=n2n1=4332=43×23=89
4. Determine Wavelength of the Refracted Ray:
- The wavelength of the refracted ray can be calculated using the formula:
λt=λμ
- Substituting the values:
λt=5000nm89=5000nm×98=450008nm=5625nm
5. Final Results:
- Wavelength of the reflected ray, λr=5000nm
- Wavelength of the refracted ray, λt=5625nm
Summary:
- The wavelength of the reflected ray is 5000nm.
- The wavelength of the refracted ray is 5625nm.
- Wavelength of incident light, λ=5000nm
- Refractive index of the first medium, n1=32
- Refractive index of the second medium, n2=43
- The wavelength of the reflected ray remains the same as that of the incident ray because reflection does not change the wavelength.
- Therefore, the wavelength of the reflected ray, λr=5000nm.
- The relative refractive index μ can be calculated using the formula:
μ=n2n1=4332=43×23=89
- The wavelength of the refracted ray can be calculated using the formula:
λt=λμ
- Substituting the values:
λt=5000nm89=5000nm×98=450008nm=5625nm
- Wavelength of the reflected ray, λr=5000nm
- Wavelength of the refracted ray, λt=5625nm
- The wavelength of the reflected ray is 5000nm.
- The wavelength of the refracted ray is 5625nm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-A (objective type question(one option is correct)))
55 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-B (objective type question(one option is correct)))
5 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Video
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
Knowledge Check
A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
A50∘B60∘C90∘D40∘
A beam of monochromatic light is refracted from vacuum into a medium of refractive index 1.5 The wavelength of refracted light will be
View SolutionA ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :
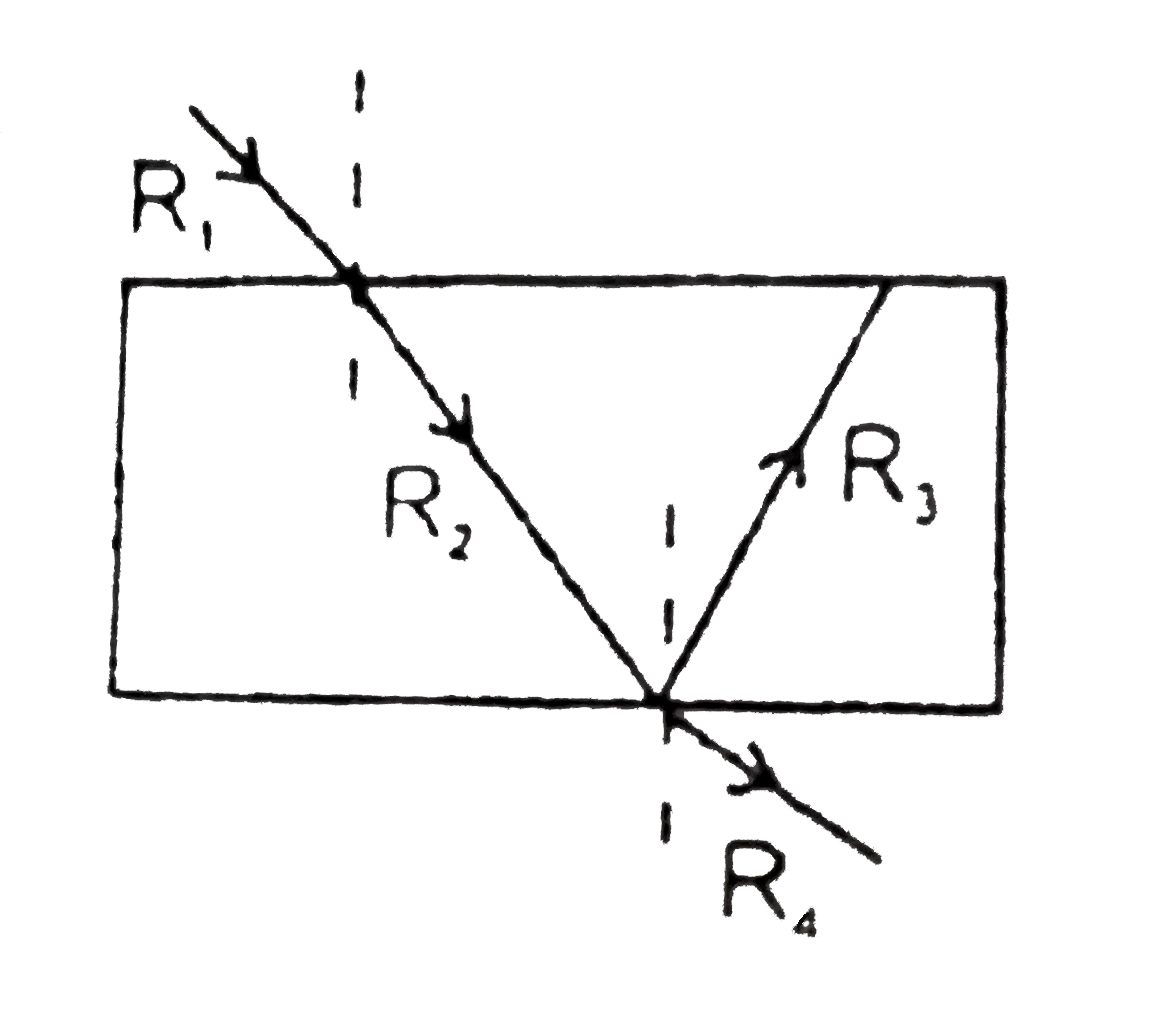
View SolutionA ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :

View SolutionIf the wavelength of light in vacuum be λ, the wavelength in a medium of refractive index n will be
View SolutionHow does the refractive index of a medium depend on the wavelength of light used ?
View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View Solution
