A conducting rod AB is bent in the form of a semicircle of radius R. It is kept in a region of uniform magnetic field B such that plane of semicircle is perpendicular to magnetic field. This rod is being moved with a constant speed v perpendicular to AB. Find the emf developed between the ends.
To find the electromotive force (emf) developed between the ends of a conducting rod bent in the form of a semicircle and moving in a magnetic field, we can follow these steps:
Step 1: Understand the Setup
We have a conducting rod AB that is bent into a semicircle with radius R. The semicircle is placed in a uniform magnetic field B such that the plane of the semicircle is perpendicular to the magnetic field. The rod is moving with a constant speed v perpendicular to the diameter AB.
Step 2: Identify the Relevant Formula
The formula for the emf (E) induced in a conductor moving in a magnetic field is given by:
E=B⋅v⋅Lequivalent⋅sin(θ)
where:
- B is the magnetic field strength,
- v is the velocity of the rod,
- Lequivalent is the equivalent length of the conductor in the magnetic field,
- θ is the angle between the velocity vector and the magnetic field vector.
Step 3: Determine the Angle
In this case, the angle θ between the velocity v (which is perpendicular to AB) and the magnetic field B (which is perpendicular to the plane of the semicircle) is 90∘. Therefore, sin(90∘)=1.
Step 4: Calculate the Equivalent Length
The equivalent length Lequivalent in this scenario is the straight-line distance between the ends A and B of the semicircle. For a semicircle of radius R, this distance is equal to the diameter:
Lequivalent=2R
Step 5: Substitute Values into the Formula
Now, substituting the values into the emf formula:
E=B⋅v⋅(2R)⋅1
This simplifies to:
E=2BvR
Final Answer
Thus, the emf developed between the ends A and B of the rod is:
E=2BvR
We have a conducting rod AB that is bent into a semicircle with radius R. The semicircle is placed in a uniform magnetic field B such that the plane of the semicircle is perpendicular to the magnetic field. The rod is moving with a constant speed v perpendicular to the diameter AB.
The formula for the emf (E) induced in a conductor moving in a magnetic field is given by:
E=B⋅v⋅Lequivalent⋅sin(θ)
where:
- B is the magnetic field strength,
- v is the velocity of the rod,
- Lequivalent is the equivalent length of the conductor in the magnetic field,
- θ is the angle between the velocity vector and the magnetic field vector.
In this case, the angle θ between the velocity v (which is perpendicular to AB) and the magnetic field B (which is perpendicular to the plane of the semicircle) is 90∘. Therefore, sin(90∘)=1.
The equivalent length Lequivalent in this scenario is the straight-line distance between the ends A and B of the semicircle. For a semicircle of radius R, this distance is equal to the diameter:
Lequivalent=2R
Now, substituting the values into the emf formula:
E=B⋅v⋅(2R)⋅1
This simplifies to:
E=2BvR
Thus, the emf developed between the ends A and B of the rod is:
E=2BvR
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Try Yourself
42 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
55 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
A uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
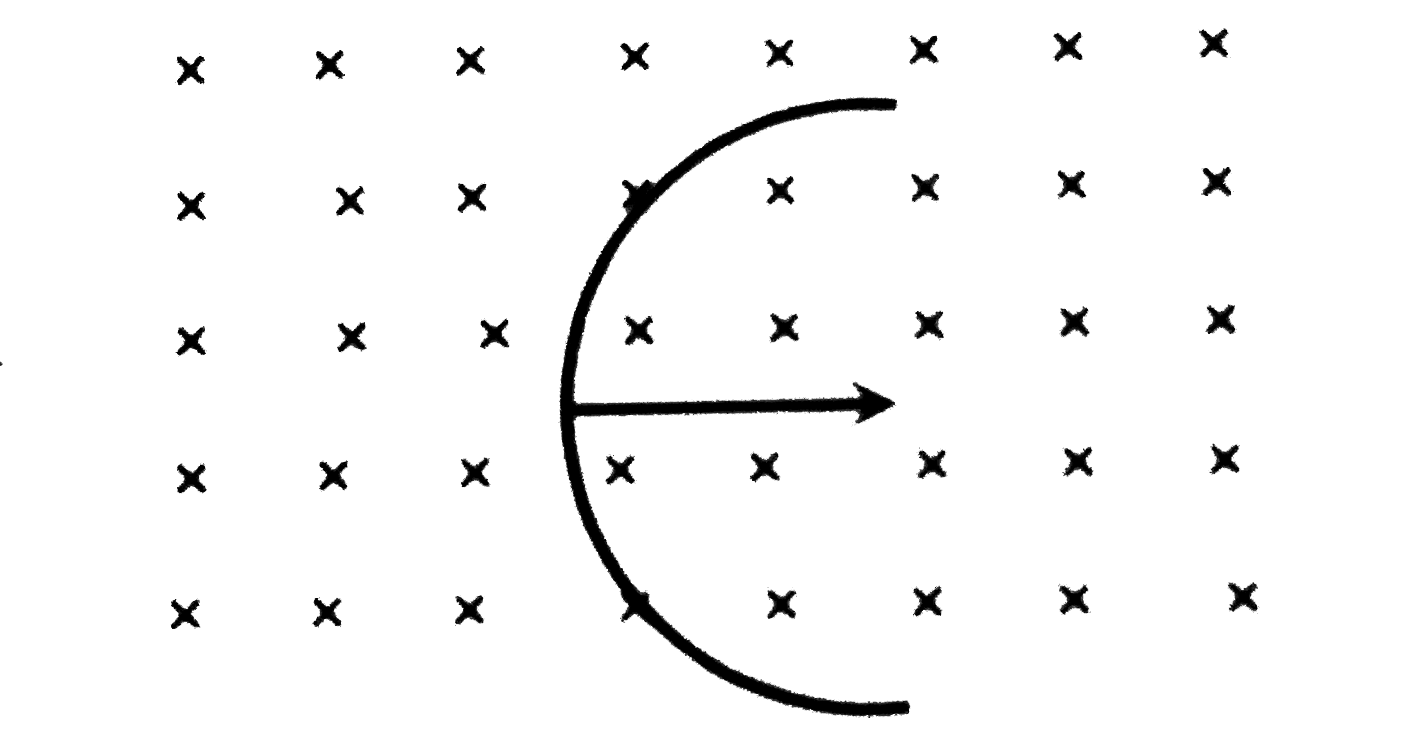
A straight wire of length L is bent into a semicircle. It is moved in a uniform magnetic field with speed v with diameter perpendicular to the field. The induced emf between the ends of the wire is
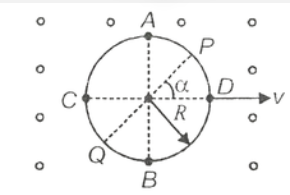
View SolutionA conducting ring of radius R is being moved in a region of uniform magnetic field as shown. Let EAB represent the potential difference between A and B then
View SolutionA copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
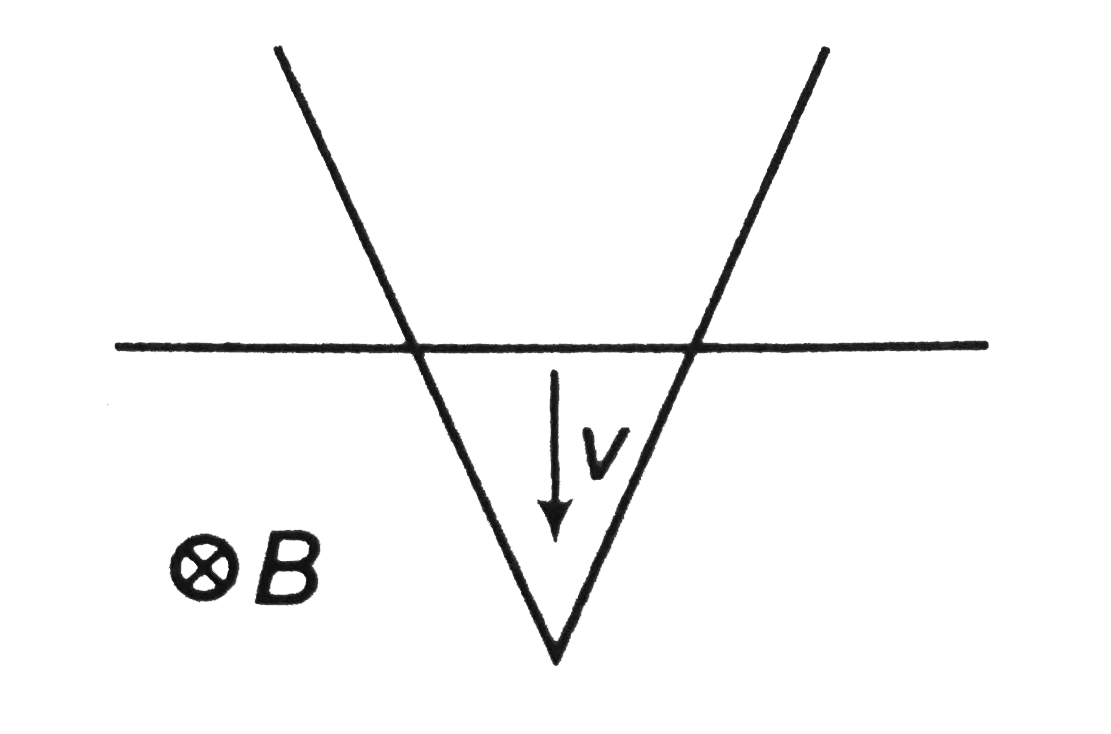
View SolutionA wire is bent in the form of a V shape and placed in a horizontal plane.There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
View SolutionIn a cylindrical region uniform magnetic field which is perpendicular to the plane of the figure is in increasing with time and a conducting rod PQ is placed in the region.If C is the centre of the circle then
View SolutionA copper rod of length l is rotated about one end perpendicular to the magnetic field B with constant angular velocity ω . The induced e.m.f between the two ends is
View Solution
