Compare the expression for magnetic energy density with electrostatic energy density stored in the space between the plates of a parallel plate capacitor.
To compare the expression for magnetic energy density with electrostatic energy density stored in the space between the plates of a parallel plate capacitor, we will derive both expressions step by step.
Step 1: Deriving Electrostatic Energy Density
1. Capacitance of a Parallel Plate Capacitor:
The capacitance (C) of a parallel plate capacitor is given by the formula:
C=ϵ0Ad
where ϵ0 is the permittivity of free space, A is the area of one plate, and d is the distance between the plates.
2. Energy Stored in the Capacitor:
The energy (U) stored in the capacitor can be expressed as:
U=12Q2C
where Q is the charge on the capacitor.
3. Relating Charge to Surface Charge Density:
The surface charge density (σ) is given by:
σ=QA⟹Q=σA
Substituting this into the energy equation gives:
U=12(σA)2C
4. Substituting Capacitance:
Substituting the expression for capacitance:
U=12(σA)2ϵ0Ad=12σ2Adϵ0
5. Electric Field Relation:
The electric field (E) between the plates is related to the surface charge density as:
E=σϵ0
Thus, we can express σ in terms of E:
σ=ϵ0E
6. Substituting for Energy:
Substituting σ back into the energy expression:
U=12(ϵ0E)2Adϵ0=12ϵ0E2Ad
7. Energy Density:
The energy density (ue) is the energy per unit volume:
ue=UV=12ϵ0E2
where V=A⋅d is the volume between the plates.
Step 2: Deriving Magnetic Energy Density
1. Magnetic Energy Density:
The magnetic energy density (ub) is given by:
ub=12B2μ0
where B is the magnetic field and μ0 is the permeability of free space.
Step 3: Comparison of Energy Densities
Now we can compare the two energy densities derived:
- Electrostatic Energy Density:
ue=12ϵ0E2
- Magnetic Energy Density:
ub=12B2μ0
Conclusion
The expressions for the energy densities are:
- Electrostatic energy density: ue=12ϵ0E2
- Magnetic energy density: ub=12B2μ0
These expressions show that both energy densities depend on the square of their respective fields (electric field E and magnetic field B) and the constants ϵ0 and μ0 which characterize the medium in which the fields exist.
The capacitance (C) of a parallel plate capacitor is given by the formula:
C=ϵ0Ad
where ϵ0 is the permittivity of free space, A is the area of one plate, and d is the distance between the plates.
The energy (U) stored in the capacitor can be expressed as:
U=12Q2C
where Q is the charge on the capacitor.
The surface charge density (σ) is given by:
σ=QA⟹Q=σA
Substituting this into the energy equation gives:
U=12(σA)2C
Substituting the expression for capacitance:
U=12(σA)2ϵ0Ad=12σ2Adϵ0
The electric field (E) between the plates is related to the surface charge density as:
E=σϵ0
Thus, we can express σ in terms of E:
σ=ϵ0E
Substituting σ back into the energy expression:
U=12(ϵ0E)2Adϵ0=12ϵ0E2Ad
The energy density (ue) is the energy per unit volume:
ue=UV=12ϵ0E2
where V=A⋅d is the volume between the plates.
The magnetic energy density (ub) is given by:
ub=12B2μ0
where B is the magnetic field and μ0 is the permeability of free space.
ue=12ϵ0E2
ub=12B2μ0
- Electrostatic energy density: ue=12ϵ0E2
- Magnetic energy density: ub=12B2μ0
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Try Yourself42videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)55videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
(b) Obtain the expression for the capacitance of a parallel plate capacitor.
View SolutionDerive the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid carrying a steady current 1. How does this magnetic energy per unit volume compare with the electrostatic energy density stored in a parallel plate capacitor ?
View SolutionDeduce an expression for the potential energy stored in a parallel plate capacitor.
View SolutionThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure, will be (area of plate =A)
 View Solution
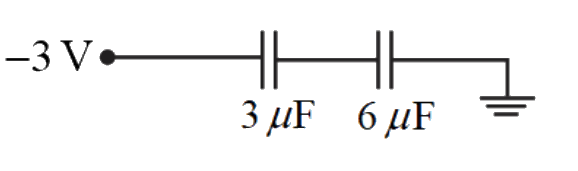
View SolutionThe total electrostatic energy stored in both the capacitors (in μJ) is
 View Solution
View SolutionIf the separation between the plates of a capacitor is 5 mm , then area of the plate of a 3 F parallel plate capacitor is
View SolutionUsing the concept of energy density, find the total energy stored in a
a. parallel plate capacitor
b. charged spherical conductor.View Solution