Two particles are projected simultaneously from two points O and O' such that d is the horizontal distance and h is the vertical distance between them as show in figure. These are projected at same inclination α with the horizontal with the same speed v. Find an expression for time at which their separation becomes minimum.

Position of particles at any time t ( taking O as origin ) is
→r1=vtcosαˆI+(vtsinα−12gt2)ˆj
→r2=(d−vtcosα)ˆi+(−h+vtsinα−12gt2)ˆj
→r=→r1−→r2(2vtcosα−d)ˆi+hˆj
⇒|→r|=√(2vtcosα−d)2+h2)
Now, drdt=0,asr=rmin
⇒12[(2tvcosα−d)2+h2]12−1×2[2vtcosα−d]×[2vcosα]=0
⇒t=d2vcosα
Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A PLANEExercise:llustration 1 :
Explore 1 Video
- MOTION IN A PLANEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A PLANEExercise:Try yourself
Explore 48 Videos
- MOCK_TEST_17Book:AAKASH INSTITUTE ENGLISHChapter:MOCK_TEST_17Exercise:Example
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
Similar Questions
Two particles are projected simultaneously from two points O and O' such that 10m is the horizontal and 5m is the vertical distance between them as shown in the figure. They are projected at the same inclination 60∘ to the horizontal with the same velocit 10ms−1. The time after which their separation becomes minimum is
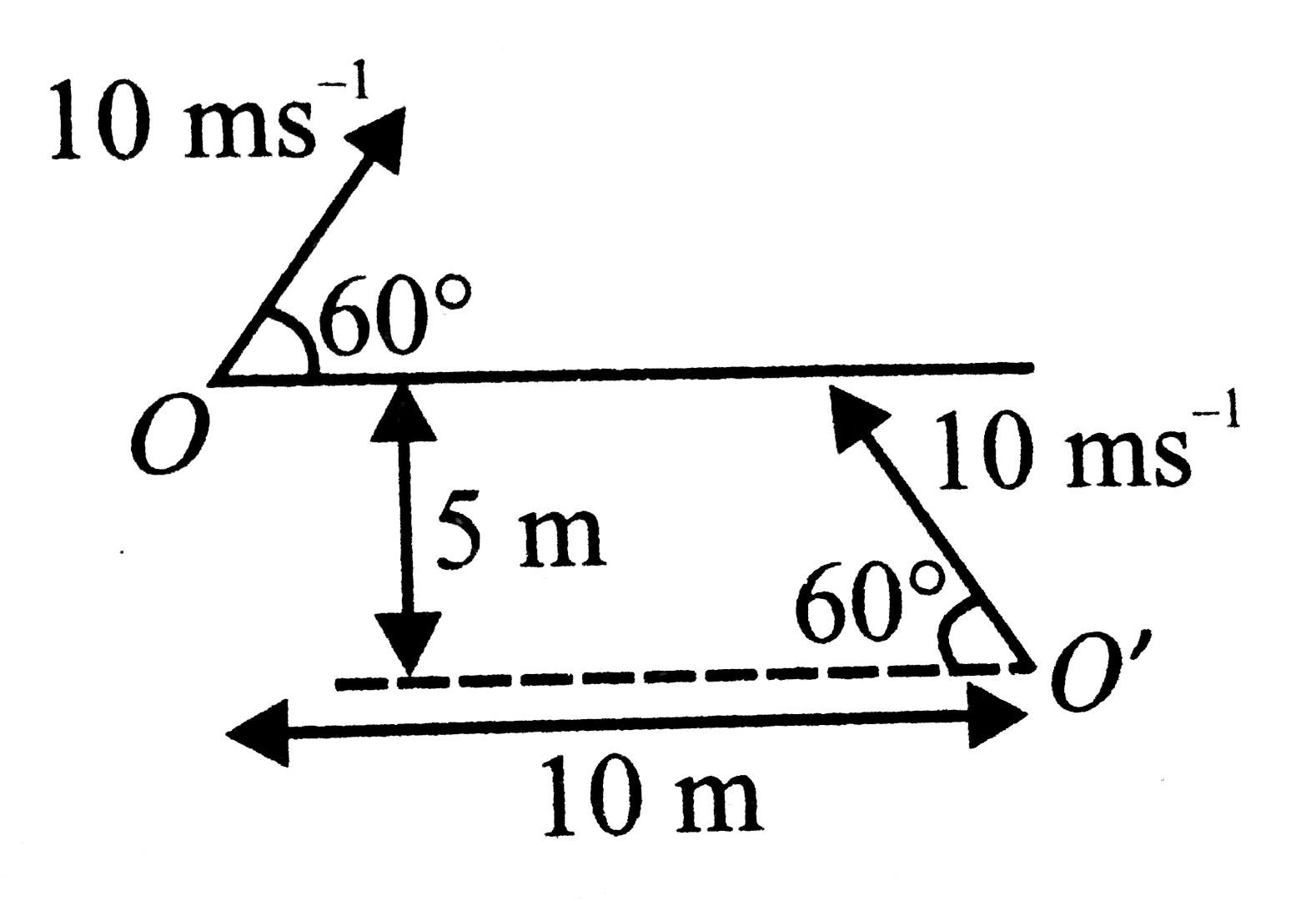
View SolutionTwo bodies are projected at angle θ and (90−θ) to the horizontal with the same speed. Find the ration of their time of flight.
View Solution
Knowledge Check
Two balls are projected at an angle θ and (90∘−θ) to the horizontal with the same speed. The ratio of their maximum vertical heights is
A1:1Btanθ:1C1:tanθDtan2θ:1
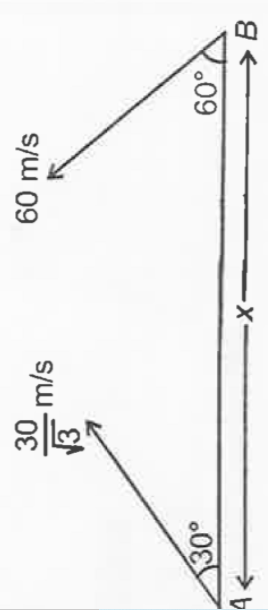
Two balls are projected from two points A and B,x metre apart as shown in figure.The time after which the horizontal distance between them become zero is
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:

View SolutionTwo balls are dropped simultaneously from two points separated by a vertical height of 6 m. The distance of separation between them after next 2s is
View SolutionTwo particles are projected simultaneously from two towers of different heights,one is horizontal with speed 10 m/s and the other at an angle 45° below the horizontal with speed v as shown in figure. The velocity v for which particles collides in air is

View SolutionTwo particles P & Q are projected simultaneously from a point O on a level ground in the same vertical plane with the same speed in directions making angle of 30∘ and 60∘ respectively with the horizontal.
View SolutionTwo particle of equal mass are projected simultaneously from the roof of a tower of height 20 m with same speed 20m//s, one horizontally and the other vertically upwards. Choose the correct alternative (s).
View SolutionTwo particles are projected simultaneously with same speed V0 in same vertical plane at angle 30∘and60∘ With the horizontal .The time at which their velocities becomes parallel is
View Solution