A ball is thrown with a speed of 20 m s−1 at an elevation angle 45∘. Find its time of flight and the horizontal range ( take g = 10ms−2)
To solve the problem of a ball thrown with a speed of 20 m/s at an elevation angle of 45 degrees, we will calculate the time of flight and the horizontal range step by step.
Step 1: Identify the given values
- Initial speed (u) = 20 m/s
- Angle of elevation (θ) = 45 degrees
- Acceleration due to gravity (g) = 10 m/s²
Step 2: Calculate the time of flight (T)
The formula for the time of flight for projectile motion is given by:
T=2usinθg
Substituting the known values:
T=2×20×sin45∘10
Since sin45∘=1√2, we can substitute this value into the equation:
T=2×20×1√210
Simplifying further:
T=40/√210=4√22=2√2 seconds
Step 3: Calculate the horizontal range (R)
The formula for the horizontal range is given by:
R=u2sin2θg
Substituting the known values:
R=202sin90∘10
Since sin90∘=1, we can simplify:
R=400×110=40 meters
Final Answers:
- Time of Flight (T) = 2√2 seconds
- Horizontal Range (R) = 40 meters
- Initial speed (u) = 20 m/s
- Angle of elevation (θ) = 45 degrees
- Acceleration due to gravity (g) = 10 m/s²
The formula for the time of flight for projectile motion is given by:
T=2usinθg
Substituting the known values:
T=2×20×sin45∘10
Since sin45∘=1√2, we can substitute this value into the equation:
T=2×20×1√210
Simplifying further:
T=40/√210=4√22=2√2 seconds
The formula for the horizontal range is given by:
R=u2sin2θg
Substituting the known values:
R=202sin90∘10
Since sin90∘=1, we can simplify:
R=400×110=40 meters
- Time of Flight (T) = 2√2 seconds
- Horizontal Range (R) = 40 meters
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Try yourself
48 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
A ball is thrown at a speed of 40 m/s at an angle of 600 with the horizontal. Find a. the maximum height reached and b. the range of te ball. Take g=10ms2.
View SolutionA ball is thrown from a field with a speed of 12.0 m/s at an angle of 450 with the horizontal. At what distance will it hit the field again ? Take g=10.0ms2
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View SolutionA particle is projected at an angle of 45∘ with a velocity of 9.8ms−1. The horizontal range will be (Take, g=9.8ms−2)
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
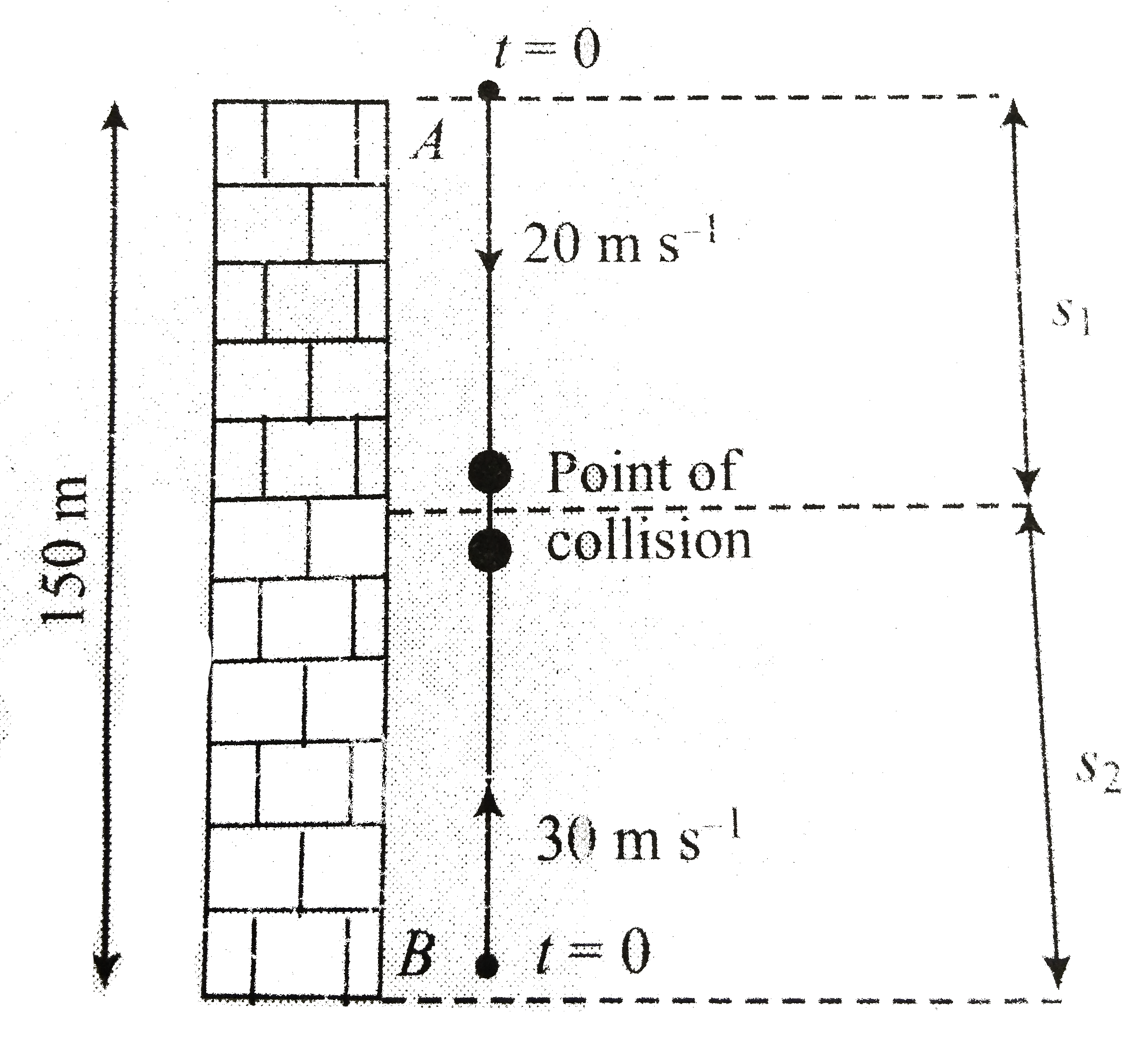 .
.
View SolutionThe maximum height attained by a ball projected with speed 20ms−1 at an angle 45∘ with the horizontal is [take g = 10ms−2]
View SolutionA ball is thrown at a speed of 20 m/s at an angle of 30∘ with the horizontal . The maximum height reached by the ball is
(Use g=10m/s2)
View SolutionA particle is projected with a speed 10√2ms−1 and at an angle 45∘ with the horizontal. The rate of change of speed with respect to time at t=1s is (g=10ms−2)
View SolutionA particle is projected with a speed of 10 m/s at an angle 37∘ with the vertical. Find (i) time of flight (ii) maximum height above ground (iii) horizontal range.
View Solution
