A man wishes to cross a river of width 120 m by a motorboat. His rowing speed in still water is 3m/s and his maximum walking speed is 1m/s. The river flows with velocity of 4m/s.
(a) Find the path which he should take to get to the point directly opposite to his starting point in the shortest time.
(b) Also, find the time which he takes to reach his destination.
First you should check whether the simmer can reach the point b directly opposite to his staring point A along the line AB or not.
The velocity v of swinmmer relative to water is 3m/s which is less than the velocity of river flow ( u= 4 m/s) . In this condition , it is not possible to have any angle θ with the AB for which the resultant of →vand→u is along AB. As u gt v, the swimmer will reach a point C somewhere to the right of point B for any angle θ he choose to start. After reaching that point C, he has to walk along the bank from C to B with walking speed v0 ( = 1 m/s) . Let him take a time t1 to reach the point C and then a time t2 to walk to B from C. Now the angle θ he has to choose in such a way that the total time takent (t1+t2)0 to reach B is minmum.
(a) t1=dvy=dvcosθandtanα=u−vsinθvcosθ
t2=BCv0=dtanαv0
Total time taken t=t1+t2
⇒t=dvcosθ+dv0(u−vsinθvcosθ)
For minimum value t,dtdthη=0


⇒(dt)(dthη)=dvsecθtanθ+udv0vsecθtanθ=dv0sec20=0
⇒tanθ(1+uv0)=vv0secθ,orsinθ=vu+v0
⇒θ=sin−1(uu+v0)=sin−1(34+1)=sin−1(35)
⇒ the swimmer should start a angle ,θ=sin(−1)(35) with AB.
(b) The total time taken is
t=dvcosθ+dv0(u−vsinθvcosθ)=1203(45)+1201⎛⎜
⎜⎝4−3×(35)3×(45)⎞⎟
⎟⎠=160s
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Video
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Try yourself
48 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
A man can swim at the rate of 5kmh−1 in still water A. One km wide river flows at the rate of 3kmh−1 . The man wishes to swim across the river directly opposite to the starting point. How much time will be take to cross the river
View SolutionThe velocity of a boat in still water is 10 m/s. If water flows in the river with a velocity of 6 m/s what is the difference in times taken to cross the river in the shortest path and the shortest time. The width of the river is 80 m.
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
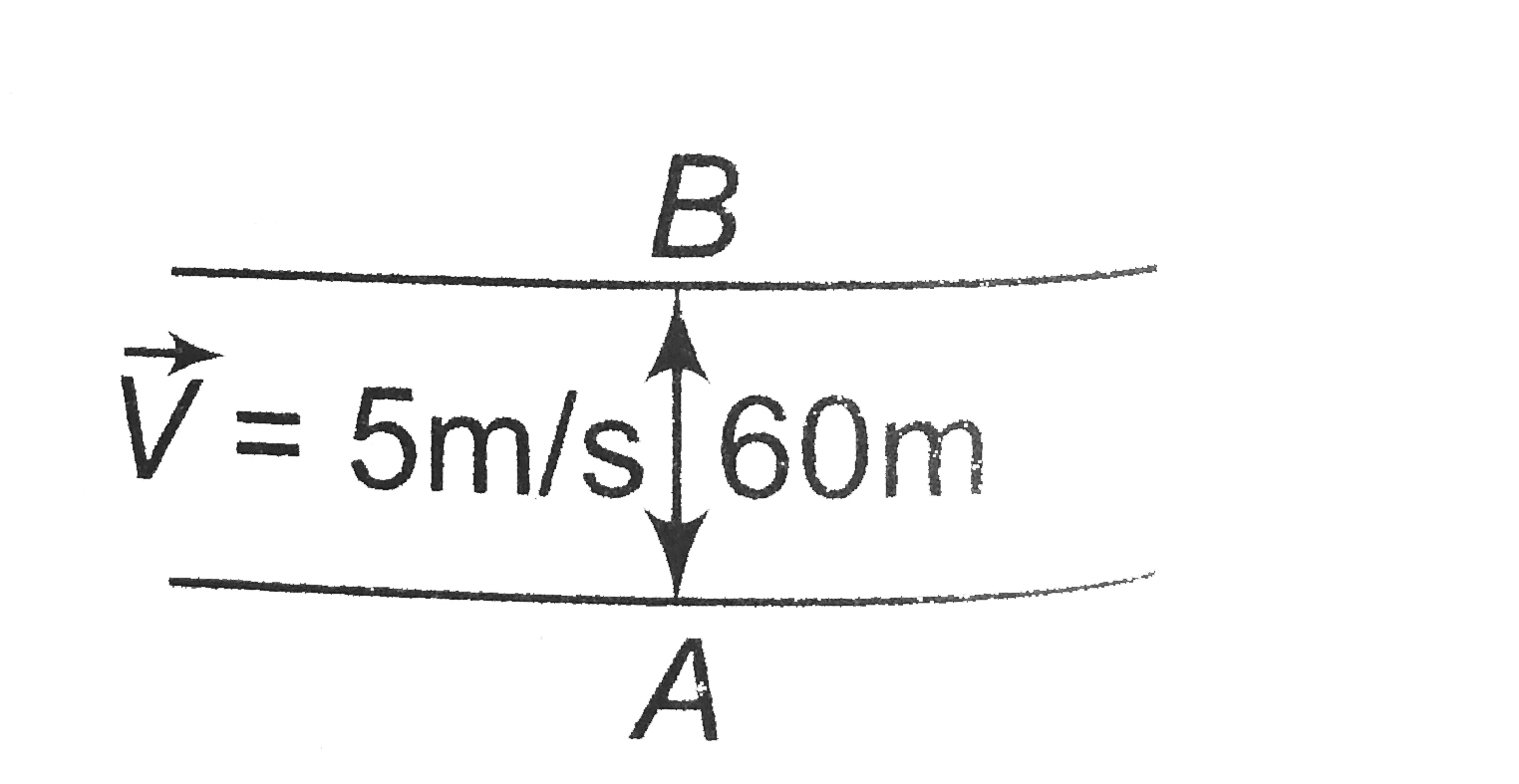
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5sec. his velocity in still water should be
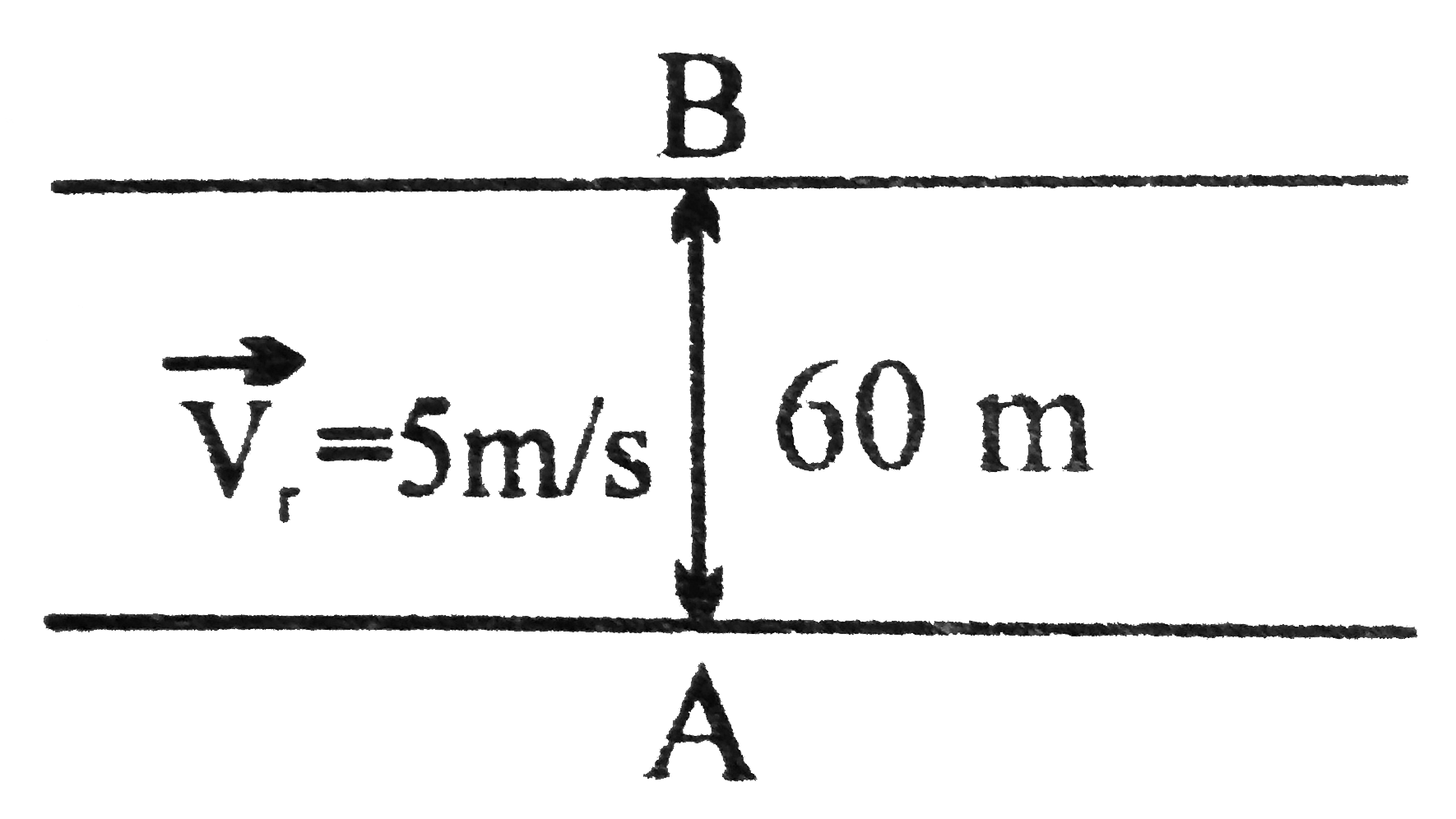
View SolutionA man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be

View SolutionVelocity of boat in still water is 13 m/s. If water flows ina river with a velocity of 5 m/s. What is the difference in times taken by him to cross the river in the shortest path and in the shortest time. If the width of the river is 10 m.
View SolutionA swimmer wishes to cross a 500m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View SolutionA swimmer wishes to cross a 500−m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
View SolutionA man can swim in still water at 4m/s river is flowing at 2m/s. the angle with downstream at which he should swim to cross the river minimum drift is
View SolutionA swimmer wants to cross a 200 m wide river which is flowing at a speed of 2 m/s. the velocity of the swimmer with respect to the river is 1 m/s. how far from the point directly opposite to the starting point does the swimmer reach the opposite bank ?
View Solution
