Prove that the area of the parallelogram with diagonal →a and →b is 12∣∣→a×→b∣∣
Let ABCD is a parallelogram with A as the origin. Let the position vector of B and D be →p and →q respectively. Then
−−→AB=→p and −−→AD=→q
But −−→BC=−−→AD Therefore −−→BC=→q
By triangle law of addition
−−→AB+−−→BC=−−→AC
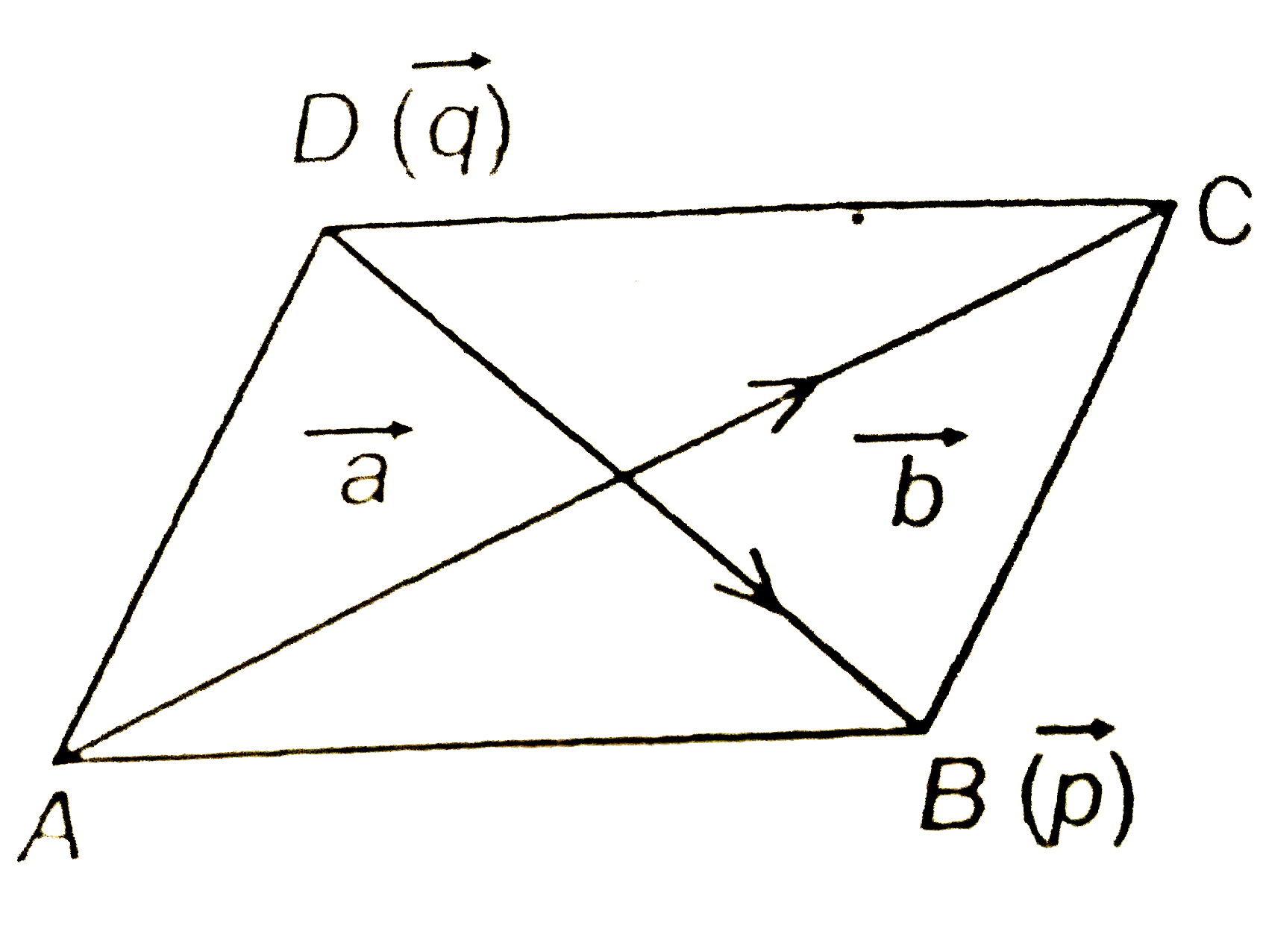
→p+→q=−−→AC
→p+→q=→a .......(i)
−−→BD=postion vector of D-positon vector of B.
⇒ →b=→q−→p .......(ii)
Adding (i) and (ii), we get
2→q=→a+→b⇒→q=12(→a+→b)
Subtracting (ii) from (i), we get
2→p=→a−→b⇒→p=12(→a−→b)
Now →p×→q=12(→a−→b)×12(→a+→b)
⇒→p×→q=14[(→a−→b)×(→a+→b)]
⇒→p×→q=14[→a×→a+→a×→b−→b×→a−→b×→b]
⇒ →p×→q=14[→a×→b+→a×→b]
⇒ →p×→q=12(→a×→b)
So, the area of parallelogram ABCD =|→p×→q|=12∣∣→a×→b∣∣
Topper's Solved these Questions
- VECTOR ALGEBRABook:AAKASH INSTITUTE ENGLISHChapter:VECTOR ALGEBRAExercise:ILLUSTRATION
Explore 1 Video
- VECTOR ALGEBRABook:AAKASH INSTITUTE ENGLISHChapter:VECTOR ALGEBRAExercise:TRY YOURSELF
Explore 20 Videos
- TRIGNOMETRIC FUNCTIONS Book:AAKASH INSTITUTE ENGLISHChapter:TRIGNOMETRIC FUNCTIONS Exercise:Section - J (Akash Challengers Question)
Explore 16 Videos
Similar Questions
Show that area of the parallelogram whose diagonals are given by →aand→b is ∣∣→a×→b∣∣2 Also, find the area of the parallelogram whose diagonals are 2i−j+kandi+3j−k.
View SolutionGiven two vectors →a=−ˆi+ˆj+2ˆkand→b=−ˆi−2ˆj−ˆk
Find
a. →a×→b then use this to find the area of the triangle.
b. The area of the parallelogram
c. The area of a paralleogram whose diagonals are
2 veca and 4vecb
View SolutionThe length of the longer diagonal of the parallelogram constructed on 5→a+2→band→a−3→b, if it is given that |→a|=2√2,∣∣→b∣∣=3and→a.Vecb=π4 is
View SolutionThe length of the longer diagonal of the parallelogram constructed on 5→a+2→band→a−3→b, if it is given that |→a|=2√2,∣∣→b∣∣=3and→a.Vecb=π4 is
View SolutionShow that the components of →b parallel to →a and perpendicular to it are (→a.→b)→a→a2and((→a×→b)→a))a2 respectively.
View SolutionIf θ is the angle between unit vectors →aand→b then sin(θ2) is (A) 12∣∣→a−→b∣∣ (B) 12∣∣→a+→b∣∣ (C) 12∣∣→a×→b∣∣ (D) 1√2√1−→a.→b
View SolutionIf →aand→b are two such that |→a|=5,∣∣→b∣∣=4and∣∣→a.→b∣∣=10, find the angle between →aand→b and hence find ∣∣→a×→b∣∣
View SolutionFind →a.→bif|→a|=2,∣∣→b∣∣=5,and∣∣→a×→b∣∣=8
View SolutionThe value of the expression ∣∣→a×→b∣∣2+(→a.→b)2 is….. .
View SolutionIf a,b are the magnitudes of vectors →a & →b and →a.→b=0 the value of ∣∣→a×→b∣∣ is
View Solution
