In the given figure, which of the vectors are :
(a) Collinear
(b) Equal
(C ) Colinitial
To solve the given problem, we need to analyze the vectors A, B, C, D, and E based on the definitions of collinear, equal, and colinitial vectors.
1. Identify Collinear Vectors:
- Definition: Collinear vectors are vectors that lie along the same line or are parallel to each other.
- Analysis: In the figure, we observe that vectors A and B are parallel to each other, as well as vectors B and C. Therefore, we can conclude that vectors A, B, and C are collinear.
2. Identify Equal Vectors:
- Definition: Equal vectors have the same magnitude and direction.
- Analysis: Upon examining the vectors in the figure, we see that vectors C and E have the same magnitude and direction. Thus, we can conclude that C and E are equal vectors.
3. Identify Colinitial Vectors:
- Definition: Colinitial vectors are vectors that have the same initial point.
- Analysis: In the figure, vectors A, B, C, and D all originate from the same starting point. Therefore, we can conclude that A, B, C, and D are colinitial vectors.
Final Conclusion:
- (a) Collinear vectors: A, B, C
- (b) Equal vectors: C, E
- (c) Colinitial vectors: A, B, C, D
- Definition: Collinear vectors are vectors that lie along the same line or are parallel to each other.
- Analysis: In the figure, we observe that vectors A and B are parallel to each other, as well as vectors B and C. Therefore, we can conclude that vectors A, B, and C are collinear.
- Definition: Equal vectors have the same magnitude and direction.
- Analysis: Upon examining the vectors in the figure, we see that vectors C and E have the same magnitude and direction. Thus, we can conclude that C and E are equal vectors.
- Definition: Colinitial vectors are vectors that have the same initial point.
- Analysis: In the figure, vectors A, B, C, and D all originate from the same starting point. Therefore, we can conclude that A, B, C, and D are colinitial vectors.
- (a) Collinear vectors: A, B, C
- (b) Equal vectors: C, E
- (c) Colinitial vectors: A, B, C, D
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - ILLUSTRATION
1 Videos
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - TRY YOURSELF
20 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
16 Videos
Similar Questions
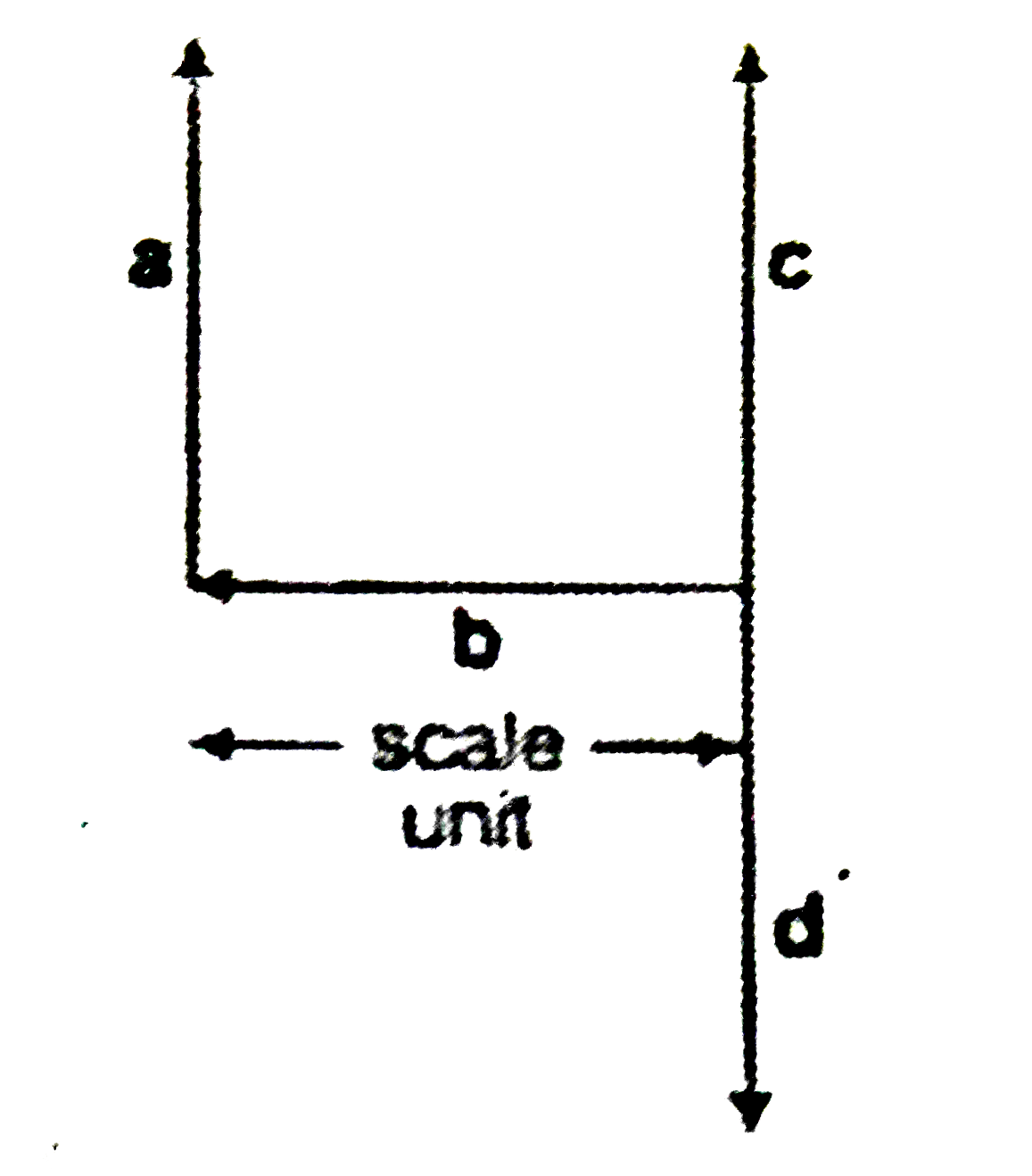
In the following figure, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Co-initial
(iv) collinear but not equal .
View SolutionIn the adjoining figure which of the vector are: equal

View SolutionIn the adjoining figure which of the vector are: collinear

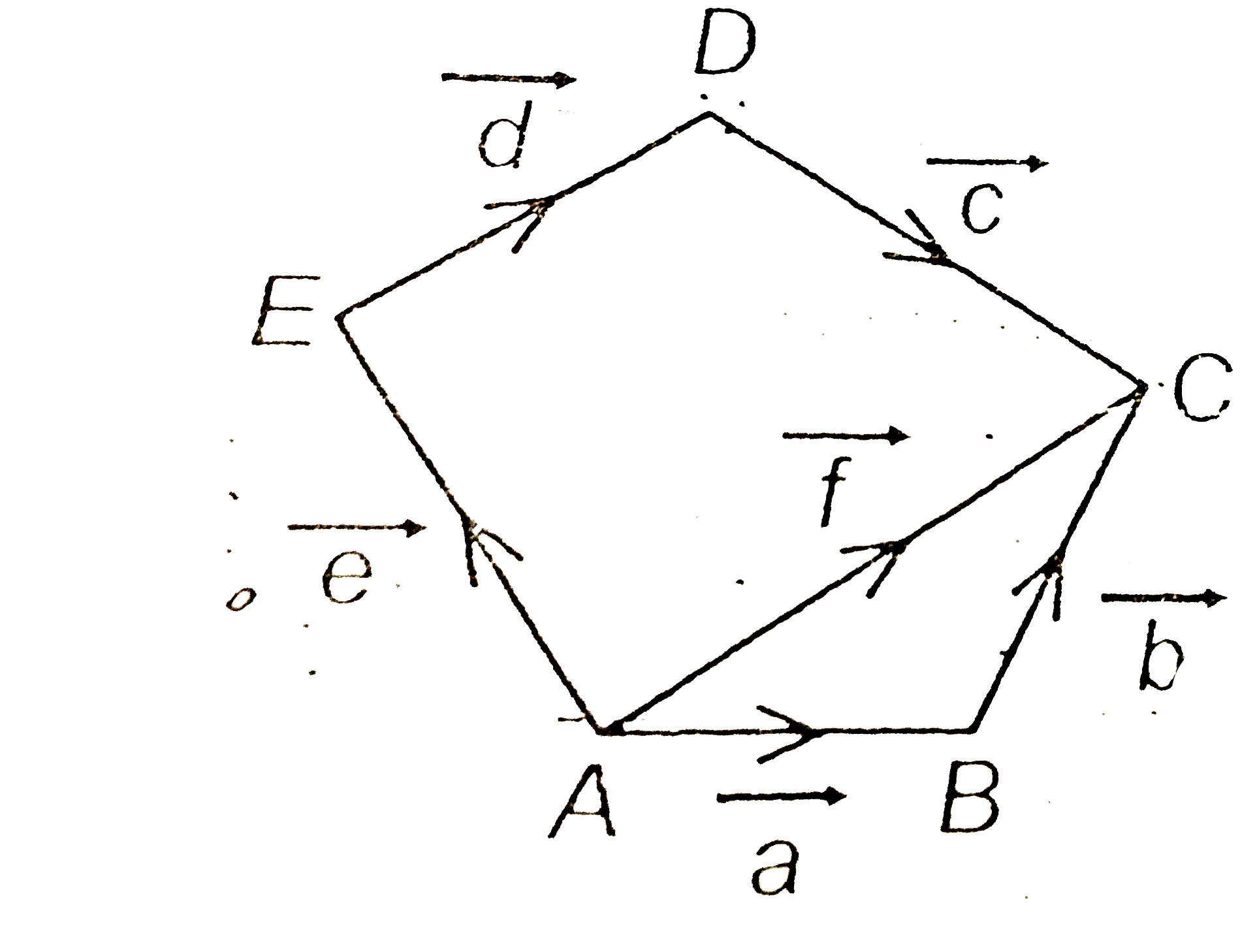
View SolutionIn the given figure, which of the following vector are
(a) collinear and equal (if ABCD are regular pentagon)
(b) coinitial vectors.
View SolutionIn fig 23.3, which of the vectors are: i.Collinear ii. Equal iii. Co-initial
View SolutionIn the given figure, ABCDEF is a regular hexagon, which vectors are:
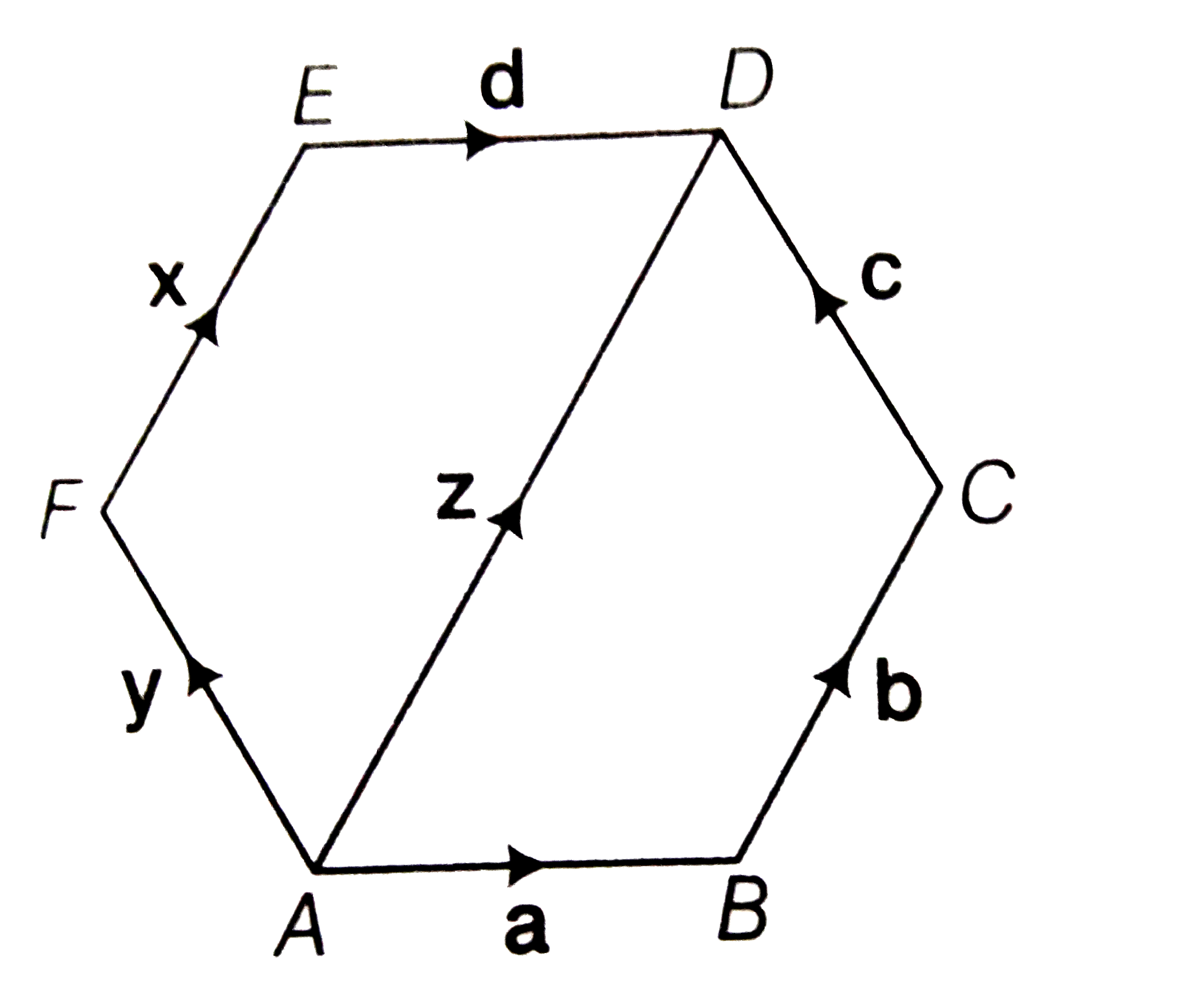
(i) Collinear
(ii) Equal
(iii) Coinitial
(iv) Collinear but not equal.
View SolutionIn Fig. ABCD is a regular hexagon, which vectors are: (i) Collinear (ii) Equal (iii) Coinitial (iv) Collinear but not equal
View SolutionIn the given figure identify the following vectors: collinear but not equal
View SolutionIn the given figure identify the following vectors: equal
View SolutionIn the given figure, vectors which are
Collinear
Equal
Collinear but not equal.

View Solution
