Question

Find the image of the line $\frac{x-1}{3}=\frac{y-2}{4}=\frac{z-3}{5}$ on the plane $x-2y+z+2=0$.

Explanation

Let B(p', q', r') be the image of A(p, q, r) with respect ot
the given plane `2x +y + z = 6.`
`rArr` AB is perpendicular to the given plane and so its
equation is given by
`(x-p)/2=(y-q)/1=(z-r)/1`

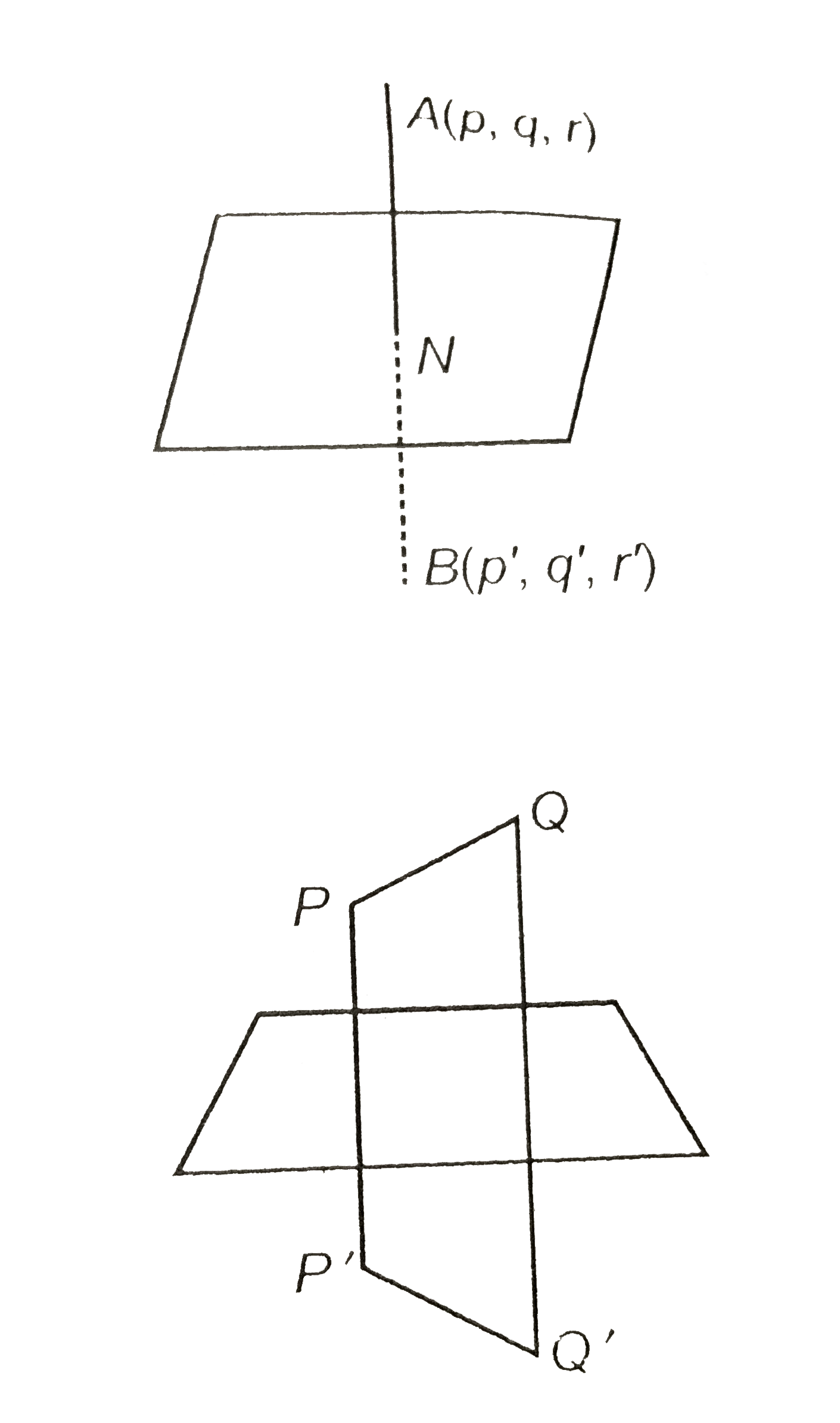
Any point on the line AB may be taken as `(p+2gamma,`
`q + lambda , r+lambda ).` Let the coordinates of B be `(p +2lambda,`
`q+lambda , r+lambda)` so that the coordinates of N are `(p +lambda,`
`q+lambda/2 , r+lambda/2)` which lies on the given plane.
Hence `2p +2lambda + q+lambda/2 + r+lambda/2 =6`
`rArr lambda =(6-2p-q-r)/3`
Hence the required image of the given point (p, q, r) with respect to the plane are
`(p+(12-4p-2p-2r)/3,q+(6-2p-q-r)/3,r+(6-2p-q-r)/3)`
`i.e. ((12-p-2p-2r)/3,(6-2p+2q-r)/3,r+(6-2p-q-2r)/3)`
The given straight line is
`(x-1)/2=(y-2)/1=(z-3)/4`
Any point on this line may be taken as `(1+4mu, 2+mu,3+4mu)`
Let two points on the line be P(1, 2, 3) and `Q(3, 3, 7)` for `mu = 0 , mu=1`
Let P' and Q' be the image of P and Q respectibely with respect ot the diven plane
then `P'(1/3,5/3,8/3) and Q' ((-11)/3, (-1)/3,11/3)`
Therefore, the equation of P' Q' is
`(x-1/3)/(12/3)=(y-5/3)/(6/3)=(z-8/3)/(-3/3)`
`rArr (3x-1)/4=(3y-5)/2=(3z-8)/(-1)`
Hence the required image of the given line `(x-1)/2=(y-2)/1=(z-3)/4` with respect ot the given plane
is `(3x-1)/4=(3y-5)/2=(3z-8)/-1.`