Using the section formula, prove that the three points and are collinear.
Let the given points are collinear and B divides AC in the ratio K : 1.
Then the coordinates of B are
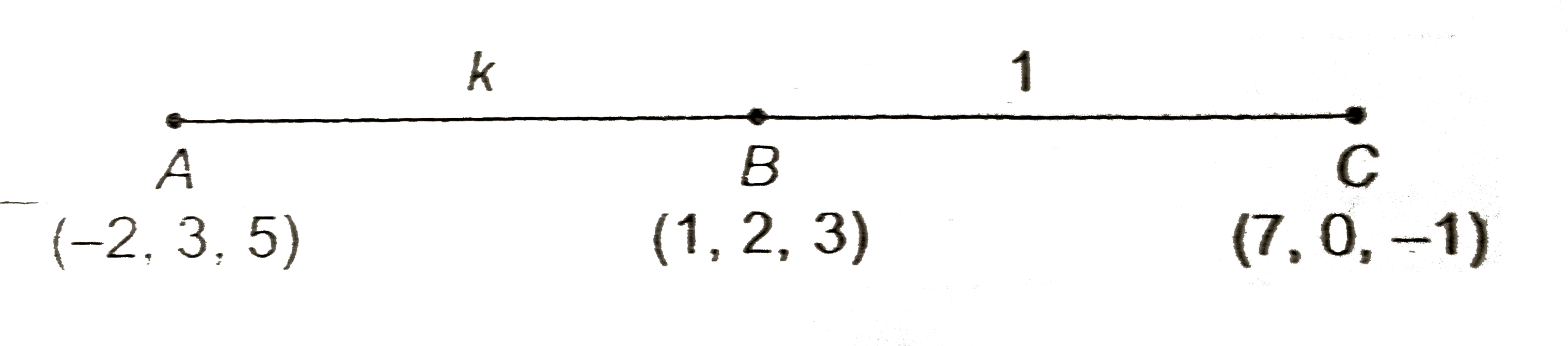
But coordinates of B are (1, 2, 3)
So,
From each of these equations, we get
Since, each of these equations give the same value of k. Therefore, the given points are collinear
and B divides AB internally in the ratio 1 : 2.
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - Illustration
4 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF
97 Videos
- STRAIGHT LINESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
5 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
16 Videos
Similar Questions
Using section formula, prove that the three points A(−2,3,5),B(1,2,3)andC(7,0,−1) are collinear.
View SolutionShow that the points A(−2,3,5),B(1,2,3)andC(7,0,−1) are collinear.
View SolutionShow that the points (−2,3,5), (1,2,3)and (7,0,−1)are collinear.
View SolutionUsing section formula, prove that the three points (−4,6,10), (2,4,6)and (14,0,−2)are collinear.
View SolutionShow that the points (−2,3,5), (1,2,3)and (7,0,−1)are collinear.
View SolutionUsing section formula, show that the points A(2,−3,4), B(−1,2,1)and C(0,13,2)are collinear.
View SolutionUsing section formula, show that the points A(2,−3,4), B(−1,2,1) and C(0,13,2) are collinear.
View SolutionProve that the points A(2,0,−3),B(1,−2,−5) and C(3,2,−1) are collinear.
View SolutionShow that the points A(2,−3,−4), B(1,2,3)and C(3,−8,−11)are collinear.
View SolutionShow that the points A(2,3,−4), B(1,−2,3)and C(3,8,−11)are collinear.
View Solution
