Question

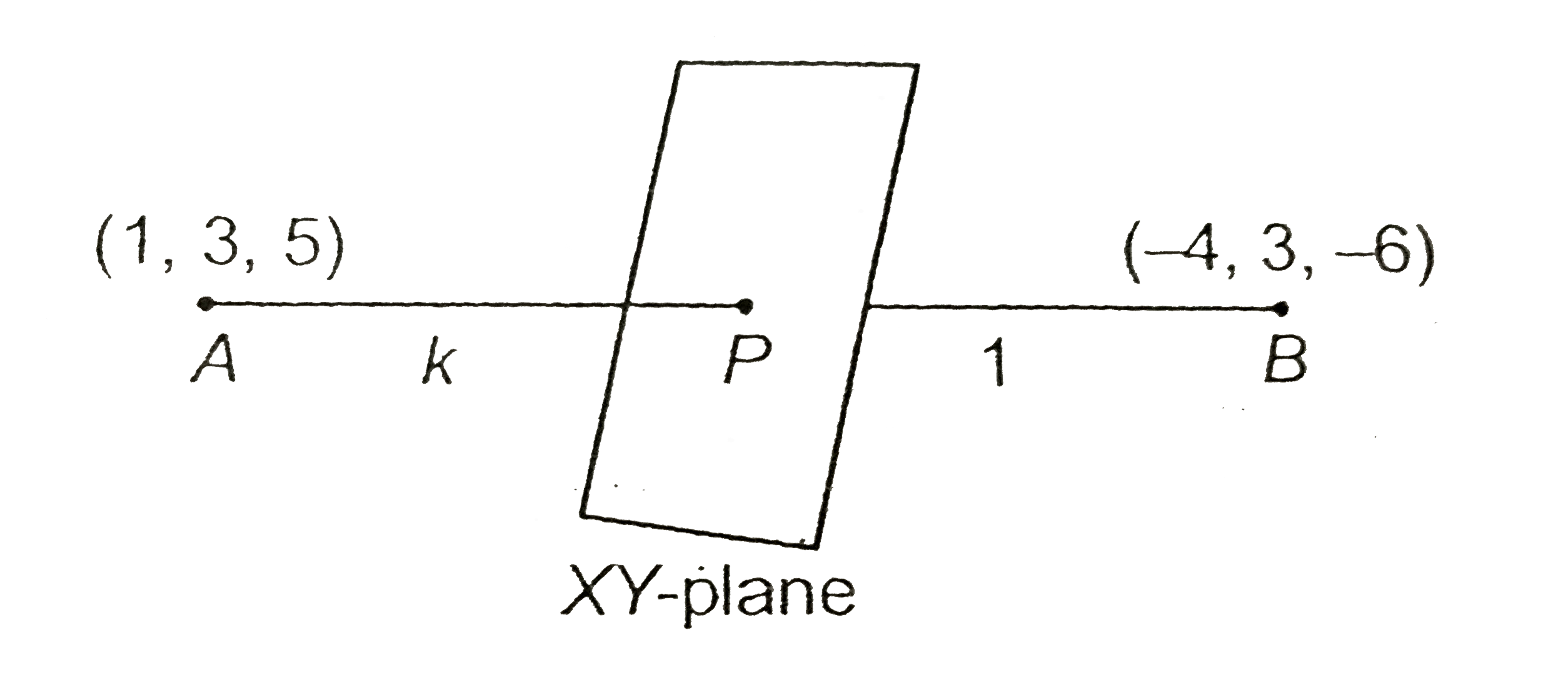
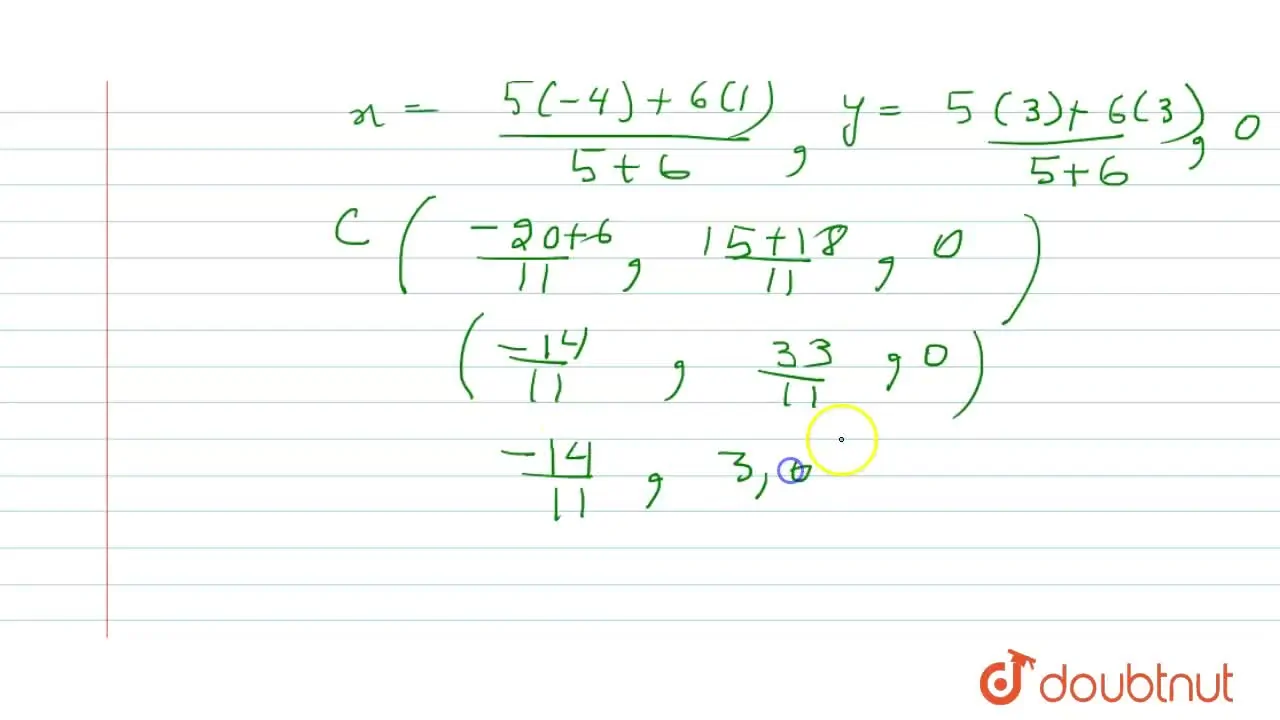Find the ratio in which the line segment joining the points (1, 3, 5) and (-4, 3, -6) is divided by
the XY-plane. Also, find the coordinates of the point of division.

Explanation

To solve the problem of finding the ratio in which the line segment joining the points $$A(1,3,5)$$ and $$B(-4,3,-6)$$ is divided by the XY-plane, as well as the coordinates of the point of division, we can follow these steps:

Step 1: Understand the Problem
The XY-plane is defined by the equation \( z = 0 \). We need to find the point \( C(x, y, 0) \) on the line segment \( AB \) that divides it in some ratio \( k:1 \).

Step 2: Use the Section Formula
The section formula in three dimensions states that if a point \( C \) divides the line segment joining points \( A(x_1, y_1, z_1) \) and \( B(x_2, y_2, z_2) \) in the ratio \( m:n \), then the coordinates of point \( C \) are given by:
\( C\left( \frac{mx_2 + nx_1}{m+n}, \frac{my_2 + ny_1}{m+n}, \frac{mz_2 + nz_1}{m+n} \right) \)

Step 3: Assign Values
Let:
- \( A(1, 3, 5) \) where \( (x_1, y_1, z_1) = (1, 3, 5) \)
- \( B(-4, 3, -6) \) where \( (x_2, y_2, z_2) = (-4, 3, -6) \)
- The ratio is \( k:1 \).

Step 4: Set Up the Equation for \( z \)
Since point \( C \) lies on the XY-plane, we set \( z = 0 \):
\( \frac{k \cdot (-6) + 1 \cdot 5}{k + 1} = 0 \)

Step 5: Solve for \( k \)
Now, we solve the equation:
\( k \cdot (-6) + 5 = 0 \)
\( -6k + 5 = 0 \)
\( 6k = 5 \)
\( k = \frac{5}{6} \)

Step 6: Find the Coordinates of Point \( C \)
Now that we have \( k \), we can find the coordinates of point \( C \) using the section formula:
- For \( x \):
\( C_x = \frac{k \cdot (-4) + 1 \cdot 1}{k + 1} = \frac{\frac{5}{6} \cdot (-4) + 1 \cdot 1}{\frac{5}{6} + 1} \)
\( = \frac{-\frac{20}{6} + 1}{\frac{5}{6} + \frac{6}{6}} = \frac{-\frac{20}{6} + \frac{6}{6}}{\frac{11}{6}} = \frac{-\frac{14}{6}}{\frac{11}{6}} = -\frac{14}{11} \)

- For \( y \):
\( C_y = \frac{k \cdot 3 + 1 \cdot 3}{k + 1} = \frac{\frac{5}{6} \cdot 3 + 1 \cdot 3}{\frac{5}{6} + 1} \)
\( = \frac{\frac{15}{6} + \frac{18}{6}}{\frac{11}{6}} = \frac{\frac{33}{6}}{\frac{11}{6}} = 3 \)

- For \( z \):
Since \( C \) lies on the XY-plane, \( C_z = 0 \).

Step 7: Final Coordinates of Point \( C \)
Thus, the coordinates of point \( C \) are:
\( C\left(-\frac{14}{11}, 3, 0\right) \)

Conclusion
The ratio in which the line segment is divided by the XY-plane is \( 5:6 \), and the coordinates of the point of division are \( \left(-\frac{14}{11}, 3, 0\right) \).