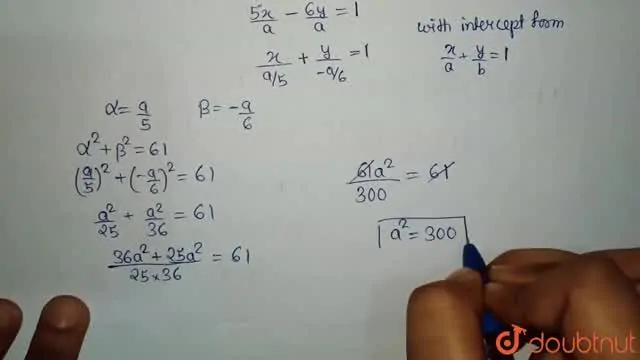If the tangent to the curve 2y3=ax2+x3 at the point (a,a) cuts off intercept αandβ on the co-ordinate axes , (where α2+β2=61) then a2 equals ______
900
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-J (Aakash Challengers Questions )8videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION- H ( Multiple True-False Type Questions ( Identify the correct statement of true (T) and False (F) of the given three statements ).)1videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF INTEGRALS EXERCISE - Assignment Section - I Aakash Challengers Questions2videos
APPLICATION OF INTEGRALS
Similar Questions
If tangent to curve 2y3=ax2+x3 at point (a, a) cuts off intercepts α,β on co-ordinate axes, where α2+β2=61, then the value of 'a' is equal to (A) 20 (B) 25 (C) 30 (D)-30
View SolutionThe abscissa of the point on the curve ay2=x3, the normal at which cuts off equal intercepts from the coordinate axes is
View SolutionIf tangents are drawn to the ellipse 2x2+3y2=6, then the locus of the mid-point of the intercept made by the tangents between the co-ordinate axes is
View SolutionFind the equation of a plane passes through the point (1,2,3) and cuts equal intercepts on the co-ordinate axes.
View SolutionIf α,β are the roots of ax2+bx+c=0 then (aα+b)−2+(aβ+b)−2=
View SolutionThe weight of an object on the surface of the Earth is 40 N. Its weight at a height equal to the radius of the Earth is
View SolutionFind the point on the curve 9y2=x3, where the normal to the curve makes equal intercepts on the axes.
View SolutionFind the points on the curve 9y2=x3 where normal to the curve makes equal intercepts with the axes.
View SolutionFind the points on the curve 9y2=x3 where normal to the curve makes equal intercepts with the axes.
View SolutionIf α,β are the roots of ax2+bx+c=0 , then α3+β3α−3+β−3 is equal to :
View Solution