The vessel is filled with 1000 litres of water at 8 a.m. The volume of water in this vessel at t hours after it is filled is observed to be v(t=1000−200t+5t2. What is the rate of change of volume (i) at 8:a .m. (ii) at noon (12:00 p.m.)?
To solve the problem, we need to find the rate of change of volume of water in the vessel at two specific times: at 8 a.m. (t = 0) and at noon (t = 4 hours). The volume of water in the vessel is given by the function:
v(t)=1000−200t+5t2
Step 1: Differentiate the Volume Function
To find the rate of change of volume with respect to time, we need to differentiate the volume function v(t) with respect to t:
dvdt=ddt(1000−200t+5t2)
Using the rules of differentiation:
- The derivative of a constant (1000) is 0.
- The derivative of −200t is −200.
- The derivative of 5t2 is 10t (using the power rule).
Thus, we have:
dvdt=0−200+10t=−200+10t
Step 2: Calculate the Rate of Change at 8 a.m. (t = 0)
Now, we will find the rate of change of volume at 8 a.m., which corresponds to t=0:
dvdt∣∣∣t=0=−200+10(0)=−200
So, the rate of change of volume at 8 a.m. is:
dvdt∣∣∣t=0=−200 liters per hour
Step 3: Calculate the Rate of Change at Noon (t = 4)
Next, we will find the rate of change of volume at noon, which corresponds to t=4:
dvdt∣∣∣t=4=−200+10(4)=−200+40=−160
So, the rate of change of volume at noon is:
dvdt∣∣∣t=4=−160 liters per hour
Final Answers
1. The rate of change of volume at 8 a.m. is −200 liters per hour.
2. The rate of change of volume at noon is −160 liters per hour.
To find the rate of change of volume with respect to time, we need to differentiate the volume function v(t) with respect to t:
- The derivative of a constant (1000) is 0.
- The derivative of −200t is −200.
- The derivative of 5t2 is 10t (using the power rule).
Now, we will find the rate of change of volume at 8 a.m., which corresponds to t=0:
Next, we will find the rate of change of volume at noon, which corresponds to t=4:
1. The rate of change of volume at 8 a.m. is −200 liters per hour.
2. The rate of change of volume at noon is −160 liters per hour.
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-A (Competition Level Questions)
50 Videos
- APPLICATION OF DERIVATIVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-B( Objective Type Questions ( One option is correct ))
31 Videos
- APPLICATION OF DERIVATIVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-J (Aakash Challengers Questions )
8 Videos
- APPLICATION OF INTEGRALS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF INTEGRALS EXERCISE - Assignment Section - I Aakash Challengers Questions
2 Videos
Similar Questions
Liquid is filled in a vessel of square base (2m×2m) upto a height of 2m as shown in figure (i). In figure (ii) the vessel is tilted from horizontal at 30∘.

What is time of fall of liquid on the ground?
View SolutionA point source S is placed at a height h from the bottom of a vessel of height H(<h). The vessel is polished at the base. Water is polished at the base. Water is gradually filled in the vessel at a constant rate αm3/s. The distance d of image of the source after reflection from mirror from the bottom of the vessel varies with time t as
View Solution
Knowledge Check
Suppose the evaporation rate of water in a lake is given by the equation E=Ta−Tb700−VTwh4, where E is the evaporation rate in gallons/day. Ta is the air temperature, Td is the dew point temperature, V is the volume of water in the table, Tw is the water temperature, and h is the number of hours the water is exposed to sunlight. Which of the following expresses Tw in terms Ta,Tb,V,E,andh?
ATw=Eh4(Ta−Tb)VBTw=700Ta−Td−Eh4VCTw=V4(Ta−Tb)Eh4DTw=VTa−Td700−Eh4Three copy machines- A,B and C- copy at the same rate and will all be used to make copies of a report. At 8:00 a.m., all 3 machines begin copying Machine A breaks down at 10:00 a.m. And is back in service at 1:00 p.m. Machine B breaks down at 12:00 p.m. (noon) and begins copying again at 3:00 p.m. All 3 machines finish copying at 5:00 p.m. when the copying of the report is complete. One of the following graphs showns n, the numbers of copies made, as a function of t, the time at any given point during the copying. Which graph is it?
A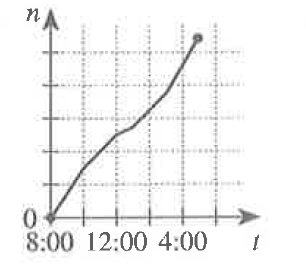 B
B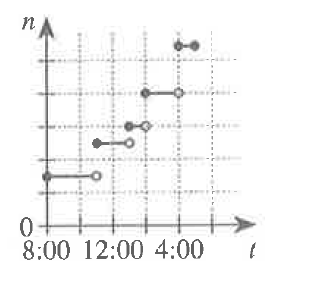 C
C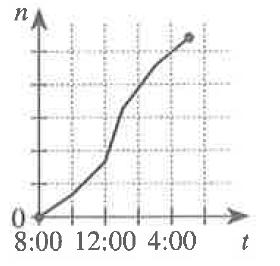 D
D
A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]A6B4C2D8
An observer observer a fish moving upwards in a cylindrical container of cross section area 1m2 filled with water up to a height of 5m. A hole is present at the botton of the container having cross section areea 1/1000m2. Find out the speed of the image of fish observed by observer when the botton hole is just opened. (Given: The fish is moving with the speed of 6m/s towards the observer, μ of water =4/3)
View SolutionA metallic disc is being heated. Its area A(in m2) at any time t(in second) is given by A=5t2+4t+8. Calculate the rate of increase in area at t=3s.
View SolutionA particle is moving on a straight line. Its velocity at time t is (8−2t)m/s. What is the total distance covered from t=0 to t=6s?
View SolutionWater is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108m3, find the number of hours it will take to fill the reservoir.
View SolutionA steel box is 2.5 m in length, 1.8 m in breadth and 1.2 m in height. Find its volume in litres.
View Solution
