Find limx→0f(x), where f(x)=⎧⎪⎨⎪⎩x−1x<00x=0x=1x>0
To find the limit limx→0f(x) for the piecewise function defined as:
f(x)=⎧⎨⎩x−1if x<00if x=01if x>0
we will evaluate the left-hand limit (LHL) and the right-hand limit (RHL) as x approaches 0.
Step 1: Calculate the Left-Hand Limit (LHL)
The left-hand limit is defined as:
limx→0−f(x)
Since x is approaching 0 from the left (i.e., x<0), we use the first case of the piecewise function:
f(x)=x−1
Thus, we have:
limx→0−f(x)=limx→0−(x−1)
Now, substituting x with values approaching 0 from the left:
=0−1=−1
So, the left-hand limit is:
LHL=−1
Step 2: Calculate the Right-Hand Limit (RHL)
The right-hand limit is defined as:
limx→0+f(x)
Since x is approaching 0 from the right (i.e., x>0), we use the third case of the piecewise function:
f(x)=1
Thus, we have:
limx→0+f(x)=1
So, the right-hand limit is:
RHL=1
Step 3: Compare the Limits
Now we compare the left-hand limit and the right-hand limit:
- LHL = -1
- RHL = 1
Since the left-hand limit is not equal to the right-hand limit, we conclude that the limit does not exist.
Conclusion
Therefore, we can say:
limx→0f(x) does not exist.
---
- RHL = 1
Topper's Solved these Questions
- LIMITS AND DERIVATIVES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LIMITS AND DERIVATIVES EXERCISE - Try yourself
64 Videos
- LIMITS AND DERIVATIVES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LIMITS AND DERIVATIVES EXERCISE - SECTION - A
50 Videos
- LIMITS AND DERIVATIVES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LIMITS AND DERIVATIVES EXERCISE - Section - j
3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - ASSIGNMENT (SECTION - J)(ANKASH CHALLENGERS QUESTIONS)
4 Videos
- MATHEMATICAL REASONINGBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATHEMATICAL REASONINGEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
Similar Questions
Find limx→1f(x), where f(x)={x+1x≠10x=1}
View SolutionFind limX→0f(x) where f(x)={xx≠05x=0}
View SolutionFind limx→0f(x) where
f(x)={x|x|x≠00x=0
View SolutionLet f(x)={1+sinxx<0x2−x+1x≥0
View SolutionCalculate limx→0f(x), where f(x)=1x2 for x>0
View SolutionLet g(x) = x - [x] - 1 and f(x)=⎧⎪⎨⎪⎩−1, x<00, x=01, x>0 [.] represents the greatest integer function then for all x, f(g(x)) = .
View SolutionDoes Limx→0f(x) exist if f(x) = ⎧⎪⎨⎪⎩x when x<00 when x=0x2 when x>0
View SolutionEvaluate limx→0f(x), where
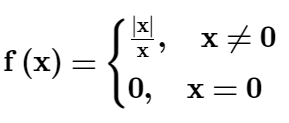
View SolutionIf F(x)=⎧⎪⎨⎪⎩−x2+1x<00x=0x2+1x>=0, .then limx→0f(x) is
View SolutionIf f(x)=⎧⎪⎨⎪⎩−1x<00x=0andg(x)=x(1−x2), then1x>0
View Solution
