Consider the sets of A={A,R,M}, B={R,A,M}, C={H,A,R,M}, D={I,N,D,I,A} and insert the symbol ⊂or⊆ between each of the following pair of set.
(i) A__B
(ii) A__C
(iii) A__D
(iv) B__A
(v) B__C
To solve the problem, we need to analyze the given sets and determine the relationship between each pair in terms of subset (⊆) or proper subset (⊂).
Given sets:
- A = {A, R, M}
- B = {R, A, M}
- C = {H, A, R, M}
- D = {I, N, D, I, A}
Now, let's analyze each pair step by step.
Step 1: Analyze A and B
- A = {A, R, M}
- B = {R, A, M}
Both sets A and B contain the same elements. Therefore, we can say:
- A ⊆ B (A is a subset of B)
- A ⊂ B (A is a proper subset of B)
Conclusion: A ⊆ B
Step 2: Analyze A and C
- A = {A, R, M}
- C = {H, A, R, M}
All elements of A (A, R, M) are present in C, but C has an additional element H. Therefore:
- A ⊆ C (A is a subset of C)
Conclusion: A ⊆ C
Step 3: Analyze A and D
- A = {A, R, M}
- D = {I, N, D, I, A}
The only common element between A and D is A. Since not all elements of A are in D, we can say:
- A ⊆ D (A is a subset of D)
Conclusion: A ⊆ D
Step 4: Analyze B and A
- B = {R, A, M}
- A = {A, R, M}
Similar to the first step, both sets contain the same elements. Therefore:
- B ⊆ A (B is a subset of A)
- B ⊂ A (B is a proper subset of A)
Conclusion: B ⊆ A
Step 5: Analyze B and C
- B = {R, A, M}
- C = {H, A, R, M}
All elements of B (R, A, M) are present in C, but C has an additional element H. Therefore:
- B ⊆ C (B is a subset of C)
Conclusion: B ⊆ C
Final Answers:
(i) A ⊆ B
(ii) A ⊆ C
(iii) A ⊆ D
(iv) B ⊆ A
(v) B ⊆ C
- A = {A, R, M}
- B = {R, A, M}
- C = {H, A, R, M}
- D = {I, N, D, I, A}
- A = {A, R, M}
- B = {R, A, M}
- A ⊆ B (A is a subset of B)
- A ⊂ B (A is a proper subset of B)
- A = {A, R, M}
- C = {H, A, R, M}
- A ⊆ C (A is a subset of C)
- A = {A, R, M}
- D = {I, N, D, I, A}
- A ⊆ D (A is a subset of D)
- B = {R, A, M}
- A = {A, R, M}
- B ⊆ A (B is a subset of A)
- B ⊂ A (B is a proper subset of A)
- B = {R, A, M}
- C = {H, A, R, M}
- B ⊆ C (B is a subset of C)
(i) A ⊆ B
(ii) A ⊆ C
(iii) A ⊆ D
(iv) B ⊆ A
(v) B ⊆ C
Topper's Solved these Questions
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-A(Objective Type Questions (One option is correct))
41 Videos
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-B(Objective Type Question(One option is correct))
13 Videos
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - EXAMPLE
24 Videos
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - J) Aakash Challengers
11 Videos
- STATISTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason
15 Videos
Similar Questions
Consider the sets of A={1,4,3,2} and B={1,2,3,4} and C={1,5,3,7} and C={1,5,3,7} and insert the symbol ⊂or⊆ between each of the following pair or set.
(i) A__B
(ii) A__C
(iii) A__B
(iv) B__A
View SolutionConsider the following sets A={1,2}, B={1,4,8}, C={1,2,4,6,8} . Insert the correct symbol of subset between each of the following pair of sets: B...C
View SolutionConsider the following sets φ, A={1,2},B={1,4,8},C={1,2,4,6,8} . Insert the correct symbol ⊂and between each of the following pair of sets: A...B
View SolutionConsider the following sets φ, A={1,2},B={1,4,8},C={1,2,4,6,8} . Insert the correct symbol ⊂and between each of the following pair of sets: A...C
View SolutionWrite down all the subsets of the following sets :
(i) {a}
(b) {a, b}
(c) {1,2,3}
(d) ϕ
View SolutionWrite the power set of each of the set (i) {a,b}, (ii) {a,b,c}.
View SolutionWhich of the following is/are not carrectly mathched pairs ?
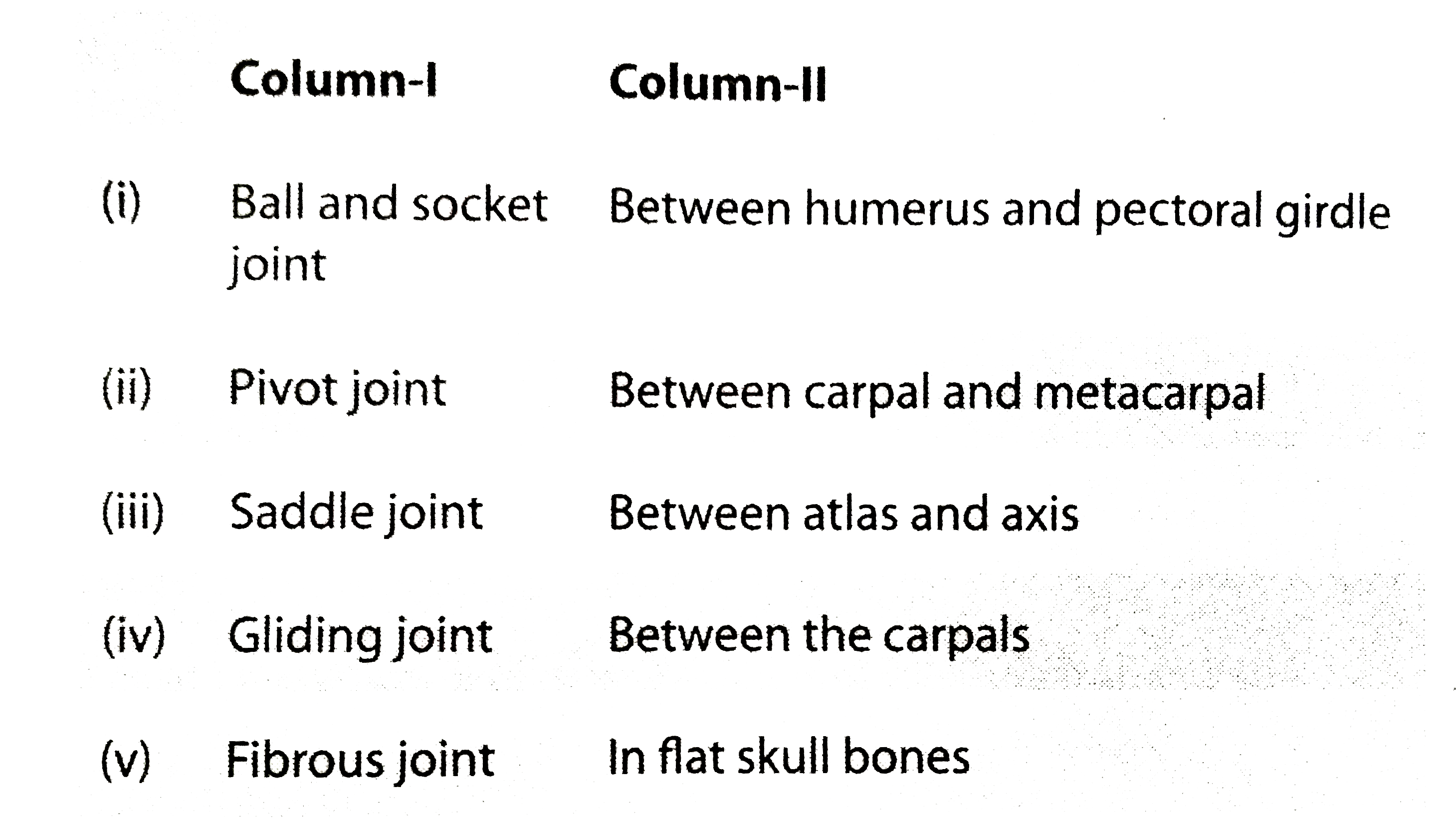
(a) (ii) and (iii)
(b) (i) and (iv)
(c) (v) only
(d) (ii) only
View SolutionGiven below is a parallelogram ABCD. Complete each statement along with the definition or property used. (I) AD= (ii) ∠DCB= (iii ) OC= (iv) ∠DAB+∠CDA=
View SolutionUsing the given diagram, express the following sets in terms of set A and B.

(i) {a,d} , (ii) {a,d,c,f}, (iii) {a,d,c,f,g,h}, (iv) {a,d,g,h}, (v) {g,h}
View SolutionGiven, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D = {Rhombuses}. State, giving reasons, whether the following are true or false.
(i) B⊂C, (ii) D⊂B, (iii) C⊆B⊆A, (iv) D⊂A, (v) B⊇C, (iv) A⊇B⊇C
View Solution
