Tangents are drawn to the circle x2+y2=12 at the points where it is met by the circle x2+y2−5x+3y−2=0 . Find the point of intersection of these tangents.
The equation of the common chord AB of the given circles is
(x2+y2−12)−(x2+y2−5x+3y−2)=0
⇒5x−3y−10=0 …(i)
Let P(h, k) be the point of intersection of the tangents drawn to the circle x2+y2=12. Then AB is the chord of contact of tangents drawn from P.
∴ The equation of AB is xh+yk=12 ...(ii)
Comparing (i) and (ii), we get
h5=k−3=−12−10
∴ Required point is (6,−185).
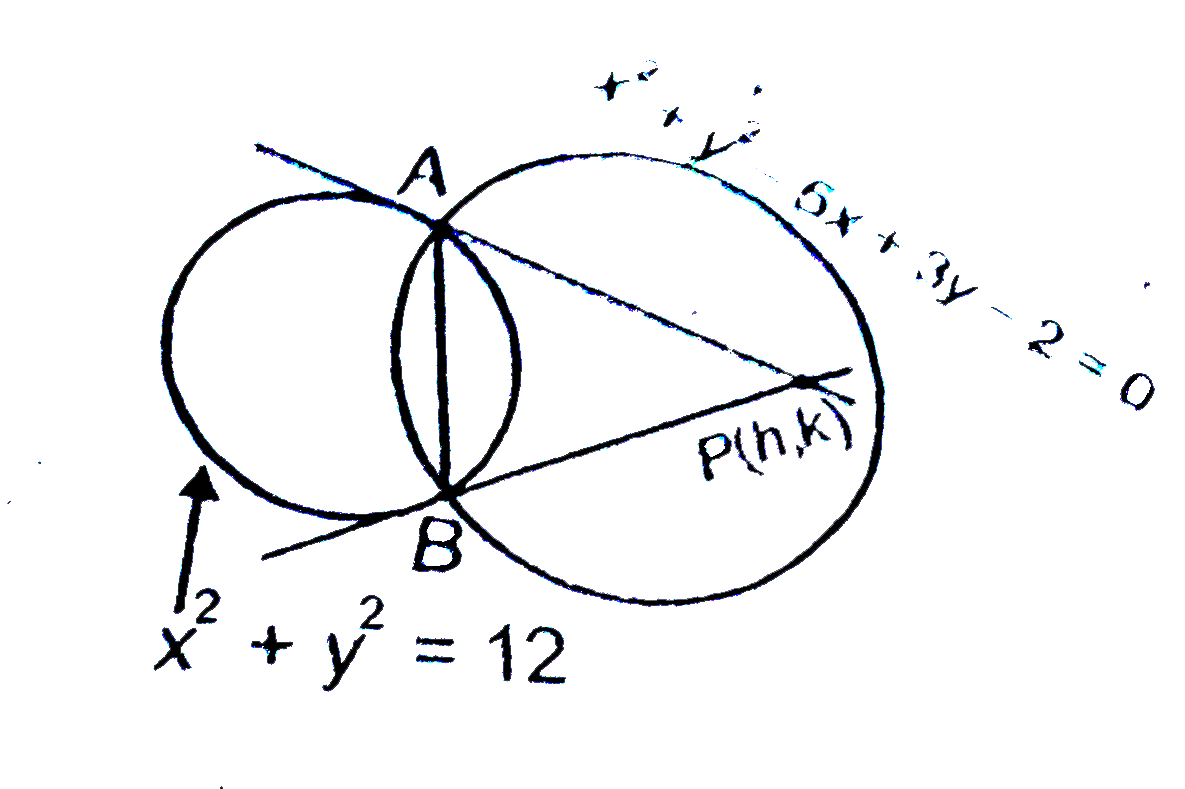
Topper's Solved these Questions
- CONIC SECTIONSBook:AAKASH INSTITUTE ENGLISHChapter:CONIC SECTIONSExercise:Try ypurself
Explore 42 Videos
- CONIC SECTIONSBook:AAKASH INSTITUTE ENGLISHChapter:CONIC SECTIONSExercise:Assignment (SECTION - A)
Explore 55 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:AAKASH INSTITUTE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:section-J (Aakash Challengers Qestions)
Explore 13 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:AAKASH INSTITUTE ENGLISHChapter:CONTINUITY AND DIFFERENTIABILITYExercise:section - J
Explore 6 Videos
Similar Questions
If the tangents are drawn to the circle x2+y2=12 at the point where it meets the circle x2+y2−5x+3y−2=0, then find the point of intersection of these tangents.
View SolutionTangents are drawn to the circle x2+y2=9 at the points where it is met by the circle x2+y2+3x+4y+2=0 . Find the point of intersection of these tangents.
View SolutionTangents are drawn to the circle x2+y2=16 at the points where it intersects the circle x2+y2−6x−8y−8=0, then the point of intersection of these tangents is
View SolutionTangents are drawn to the circle x2+y2=9 at the points where it is cut by the line 4x+3y−9=0 then the point of intersection of tangents is
View SolutionTangents are drawn to the parabola y2=4ax at the point where the line lx+my+n=0 meets this parabola. Find the point of intersection of these tangents.
View SolutionTangents are drawn to the parabola y2=4ax at the point where the line lx+my+n=0 meets this parabola. Find the point of intersection of these tangents.
View SolutionTangent are drawn to the circle x2+y2=1 at the points where it is met by the circles x2+y2−(λ+6)x+(8−2λ)y−3=0,λ being the variable. The locus of the point of intersection of these tangents is 2x−y+10=0 (b) 2x+y−10=0 x−2y+10=0 (d) 2x+y−10=0
View SolutionFind the point of intersection of the circle x2+y2−3x−4y+2=0 with the x-axis.
View SolutionThe tangent to the circle x2+y2=5 at (1,−2) also touches the circle x2+y2−8x+6y+20=0 . Find the coordinats of the corresponding point of contact.
View SolutionFrom an arbitrary point P on the circle x2+y2=9 , tangents are drawn to the circle x2+y2=1 , which meet x2+y2=9 at A and B . The locus of the point of intersection of tangents at A and B to the circle x2+y2=9 is
(a) x2+y2=(277)2 (b) x2−y2(277)2 y2−x2=(277)2 (d) none of these
View Solution

