The sum of cost of 5 eraser, 3 pencil and 1 pan is Rs. 16. The sum of cost of 2 eraser, 1 pencil and 3 pen is Rs. 19. While the cost of 1 eraser, 2 pencil and 4 pen is Rs. 25. Find cost per unit of eraser, pencil and pen.
Let x, y, z be the cost per unit, then we have
5x+3y+z=16
2x+y+2z=19
x+2y−4y=25
It can be written as
AX=B
Where, A=⎡⎢⎣531213124⎤⎥⎦,X=⎡⎢⎣xyz⎤⎥⎦,B=⎡⎢⎣161925⎤⎥⎦
Here, |A|=5(4−6)−3(8−3)+1(4−1)=−22≠0
Hence A is non-singular given equations will give unique solution.
adj A=⎡⎢⎣−2−108−519−133−7−1⎤⎥⎦
∴ A−1adj A|A|=1−22⎡⎢⎣−2−108−519−133−7−1⎤⎥⎦=⎡⎢
⎢
⎢
⎢⎣2221022−822522−19221322−322722122⎤⎥
⎥
⎥
⎥⎦
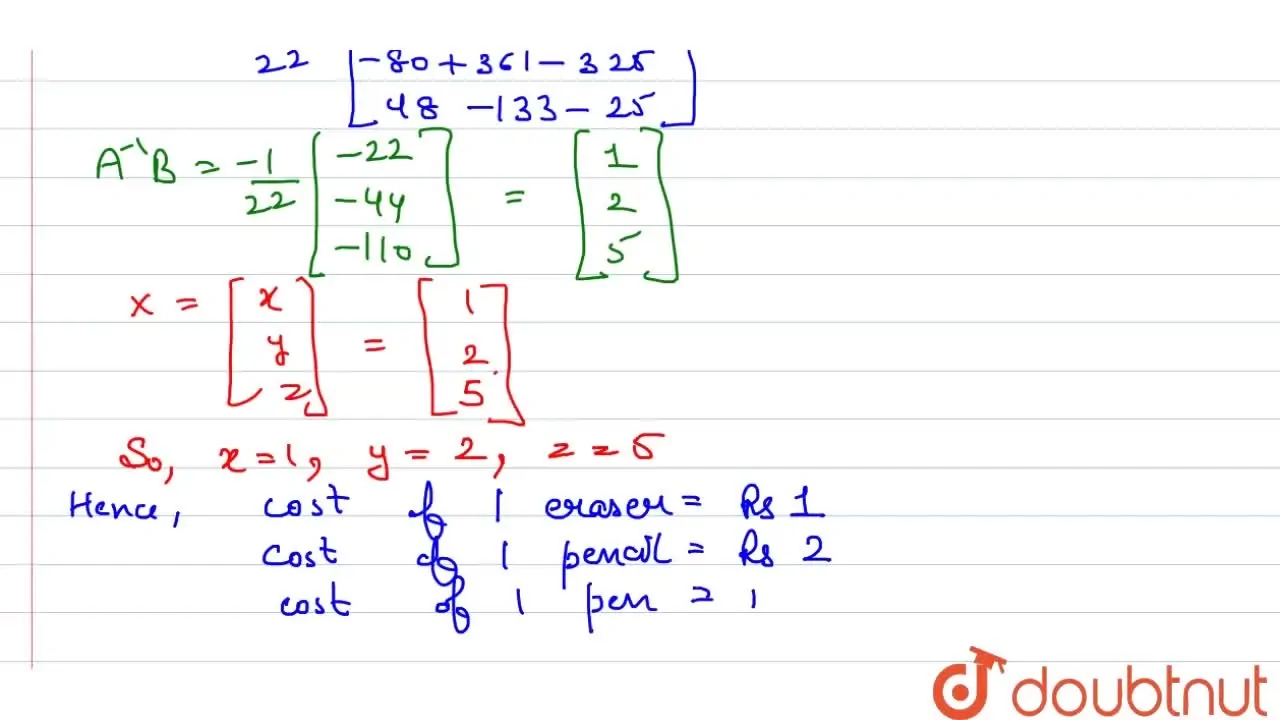
∴ X=A−1B=⎡⎢
⎢
⎢
⎢⎣2221022−822522−19221322−322722122⎤⎥
⎥
⎥
⎥⎦⎡⎢⎣161925⎤⎥⎦=⎡⎢⎣125⎤⎥⎦
∴ x=1,y=2,z=5
Cost of reaser per unit = Rs. 1
Cost of pencil per unit = R. 2
Cost of per per unit = Rs. %
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DETERMINANTS EXERCISE - Try Yourself12videos
DETERMINANTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DETERMINANTS EXERCISE - SECTION A33videos
DETERMINANTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - section - J6videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Assignment Section - J (Aakash Challengers Questions)4videos
DIFFERENTIAL EQUATIONS
Similar Questions
The cost of 3 oranges and 12 apples is Rs. 9.60 and the cost of 5 oranges and 7 apples is Rs. 6.90. Find the cost of apples per dozen.
View Solution5 pens and 6 pencils together cost Rs 9 and 3 pens and 2 pencils cost Rs 5. Find the cost of 1 pen and 1 pencil.
View Solution5 pens and 6 pencils together cost Rs 9 and 3 pens and 2 pencils cost Rs 5. Find the cost of 1 pen and 1 pencil.
View SolutionLet us consider Example 2 in Section 3.3, i.e., the cost of 2 pencils and 3 erasers is Rs 9 and the cost of 4 pencils and 6 erasers is Rs 18. Find the cost of each pencil and each eraser.
View SolutionThe cost of 17 pencils is Rs59(12). Find the cost of each pencil.
View SolutionThe cost of 1 pens is Rs 114 14 find the cost of 19 pens
View SolutionThe cost of 13 pens is Rs5812. Find the cost of each pen.
View SolutionIf 7 pencils cost Rs 35, then the cost of one dozen pencils is
View SolutionIf the cost of 20 pens is Rs 110, what is the cost of 4 pens ?
View SolutionOne pencil costs Rs. 2 and one fountain pen costs Rs. 15. What is the cost of x pencils and y fountain pens?
View Solution