A,B,C and D have mixed up their respective secret codes in an envelope in How many ways can they pick up their codes in such a manner that no one gets his own code ?
To solve the problem of how many ways A, B, C, and D can pick up their secret codes such that no one gets their own code, we will use the concept of derangements. A derangement is a permutation of a set where none of the elements appear in their original position.
1. Understanding the Problem:
We need to find the number of ways to arrange the codes of A, B, C, and D such that none of them receives their own code. This is a classic derangement problem.
2. Derangement Formula:
The formula for the number of derangements !n of n items is given by:
!n=n!(n∑i=0(−1)ii!)
For our case, n=4.
3. Calculate 4!:
First, calculate 4!:
4!=4×3×2×1=24
4. Calculate the Summation:
Now, we need to calculate the summation:
4∑i=0(−1)ii!
Breaking it down:
- For i=0: (−1)00!=1
- For i=1: (−1)11!=−1
- For i=2: (−1)22!=12
- For i=3: (−1)33!=−16
- For i=4: (−1)44!=124
Now, summing these values:
1−1+12−16+124
5. Finding a Common Denominator:
The common denominator for 2,6, and 24 is 24:
- Convert each term:
- 1=2424
- −1=−2424
- 12=1224
- −16=−424
- 124=124
Now, summing these:
24−24+12−4+124=924=38
6. Calculate the Derangement:
Now, substituting back into the derangement formula:
!4=4!×38=24×38=9
Final Answer:
Thus, the total number of ways A, B, C, and D can pick up their codes such that no one gets their own code is 9.
We need to find the number of ways to arrange the codes of A, B, C, and D such that none of them receives their own code. This is a classic derangement problem.
The formula for the number of derangements !n of n items is given by:
!n=n!(n∑i=0(−1)ii!)
For our case, n=4.
First, calculate 4!:
4!=4×3×2×1=24
Now, we need to calculate the summation:
4∑i=0(−1)ii!
Breaking it down:
- For i=0: (−1)00!=1
- For i=1: (−1)11!=−1
- For i=2: (−1)22!=12
- For i=3: (−1)33!=−16
- For i=4: (−1)44!=124
1−1+12−16+124
The common denominator for 2,6, and 24 is 24:
- Convert each term:
- 1=2424
- −1=−2424
- 12=1224
- −16=−424
- 124=124
24−24+12−4+124=924=38
Now, substituting back into the derangement formula:
!4=4!×38=24×38=9
Thus, the total number of ways A, B, C, and D can pick up their codes such that no one gets their own code is 9.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Try Yourself
65 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section A Objective type questions (One option is correct )
51 Videos
- MATRICESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions
3 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
11 Videos
Similar Questions
There are 6 students A,B,C,D,E,F. In how many ways can they be seated in a line so that C and D do not sit together?
View SolutionSuppose n different games are to be given to n children. In how many ways can this be done so that eactly one child gets no game.
View SolutionIn how many ways can 5 different books be tied up in three bundles?
View SolutionIn how many ways can 20 identical toys be distributed among 4 children so that each one gets at least 3 toys?
View SolutionHow many bases code for one amino acid?
View SolutionMatch List I with List II and pick up the correct choice from the under assigned codes
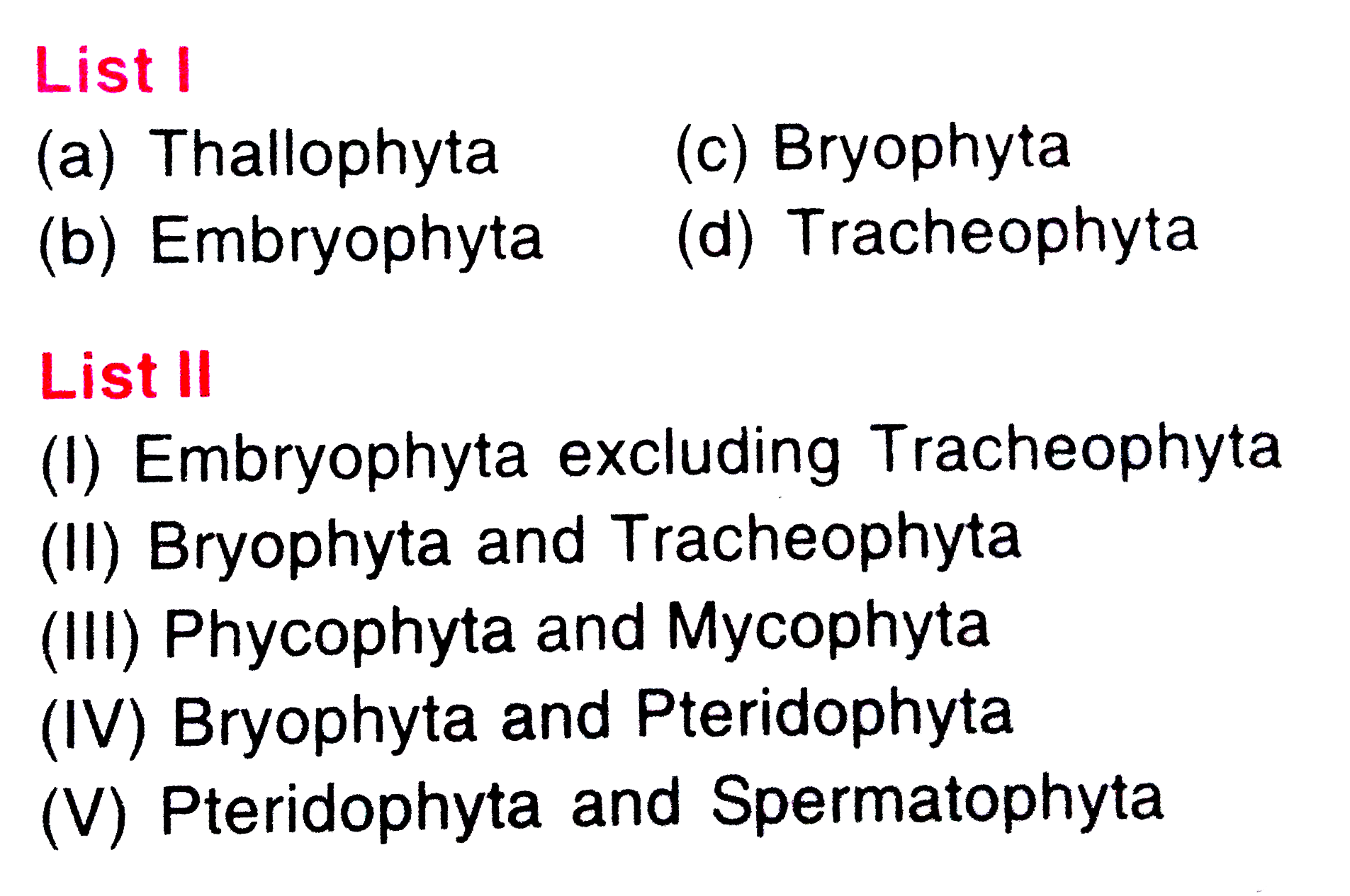
View SolutionSix very good friends decide they will have lunch together ecery day . In how many different ways can they line up in the line ?
View SolutionIn how many ways can the 7 letters A, B, C, D, E, F, and G be arranged so that C and E are never together?
View SolutionRamesh has 6 friends. In how many ways can be invite one or more of them at a dinner ? (A) 61 (B) 62 (C) 63 (D)64
View SolutionSeven people leave their bags outside at temple and returning after worshiping picked one bag each at random. In how many ways at least one and at most three of them get their correct bags?
View Solution
