Find the mean , mean deviation about the mean , variance and standard deviation for the following data
4,15,14,12,6,8,11
To solve the problem, we will follow these steps:
Step 1: Calculate the Mean
The mean (average) is calculated using the formula:
Mean=∑xin
Where ∑xi is the sum of all observations and n is the number of observations.
Given data: 4,15,14,12,6,8,11
Calculating the sum:
4+15+14+12+6+8+11=70
Number of observations n=7.
Now, calculating the mean:
Mean=707=10
Step 2: Calculate the Mean Deviation about the Mean
Mean deviation is calculated using the formula:
Mean Deviation=∑|xi−¯x|n
Where ¯x is the mean calculated in Step 1.
Calculating |xi−¯x|:
- For x1=4: |4−10|=6
- For x2=15: |15−10|=5
- For x3=14: |14−10|=4
- For x4=12: |12−10|=2
- For x5=6: |6−10|=4
- For x6=8: |8−10|=2
- For x7=11: |11−10|=1
Now summing these values:
6+5+4+2+4+2+1=24
Now, calculating the mean deviation:
Mean Deviation=247≈3.43
Step 3: Calculate the Variance
Variance is calculated using the formula:
Variance=∑(xi−¯x)2n
Calculating (xi−¯x)2:
- For x1=4: (4−10)2=36
- For x2=15: (15−10)2=25
- For x3=14: (14−10)2=16
- For x4=12: (12−10)2=4
- For x5=6: (6−10)2=16
- For x6=8: (8−10)2=4
- For x7=11: (11−10)2=1
Now summing these values:
36+25+16+4+16+4+1=102
Now, calculating the variance:
Variance=1027≈14.57
Step 4: Calculate the Standard Deviation
Standard deviation is the square root of the variance:
Standard Deviation=√Variance=√14.57≈3.82
Final Results
- Mean: 10
- Mean Deviation: 3.43
- Variance: 14.57
- Standard Deviation: 3.82
---
The mean (average) is calculated using the formula:
4+15+14+12+6+8+11=70
Mean=707=10
Mean deviation is calculated using the formula:
- For x1=4: |4−10|=6
- For x2=15: |15−10|=5
- For x3=14: |14−10|=4
- For x4=12: |12−10|=2
- For x5=6: |6−10|=4
- For x6=8: |8−10|=2
- For x7=11: |11−10|=1
6+5+4+2+4+2+1=24
Mean Deviation=247≈3.43
Variance is calculated using the formula:
- For x1=4: (4−10)2=36
- For x2=15: (15−10)2=25
- For x3=14: (14−10)2=16
- For x4=12: (12−10)2=4
- For x5=6: (6−10)2=16
- For x6=8: (8−10)2=4
- For x7=11: (11−10)2=1
36+25+16+4+16+4+1=102
Variance=1027≈14.57
Standard deviation is the square root of the variance:
- Mean: 10
- Mean Deviation: 3.43
- Variance: 14.57
- Standard Deviation: 3.82
Topper's Solved these Questions
- STATISTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-A Competition Level
10 Videos
- STATISTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-B Linked Comprehension
5 Videos
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-I(Aakash Challengers Questions)
4 Videos
- STRAIGHT LINESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
5 Videos
Similar Questions
Calculate the mean, variance and standard devation for the following data :
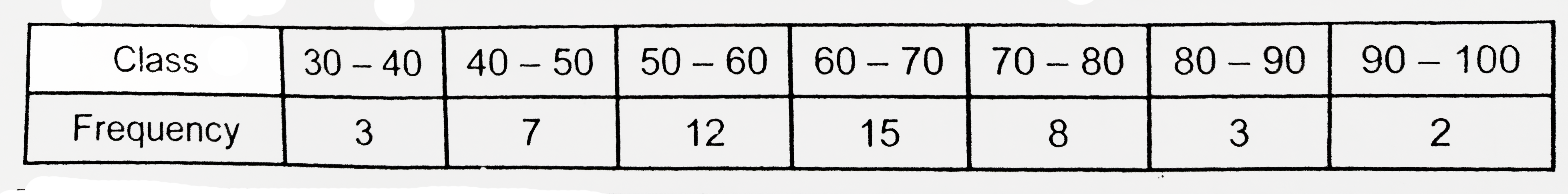
View SolutionFind the mean variance and standard deviation for the following data: 2,4,5,6,8,17
View SolutionFind the mean, variance and standard deviation for the following data: 6,7,10,12,13,4,8,12
View SolutionFind the variance and standard deviation of the following data:

View SolutionFind the variance and standard deviation from the following data:

View SolutionFind the variance and standard deviation for the following data: 4,6,10,12,14,18,20
View SolutionFind the variance and standard deviation of the following data 5,12,3,18,6,8,2,10
View SolutionFind the mean and standard deviation from the following data :

View SolutionCalculate variance and standard deviation of the following data : 10, 12, 8, 14, 16
View SolutionFind the standard deviation for the following data :5,9,8,12,6,10,6,8
View Solution
