Solutions of sin−1(sinx)=sinx are , if x∈(0,2π)
A
4 real roots
B
2 positive real roots
C
2 negative real roots
D
5 real roots
Video Solution
Text Solution
The correct Answer is:D
By graph
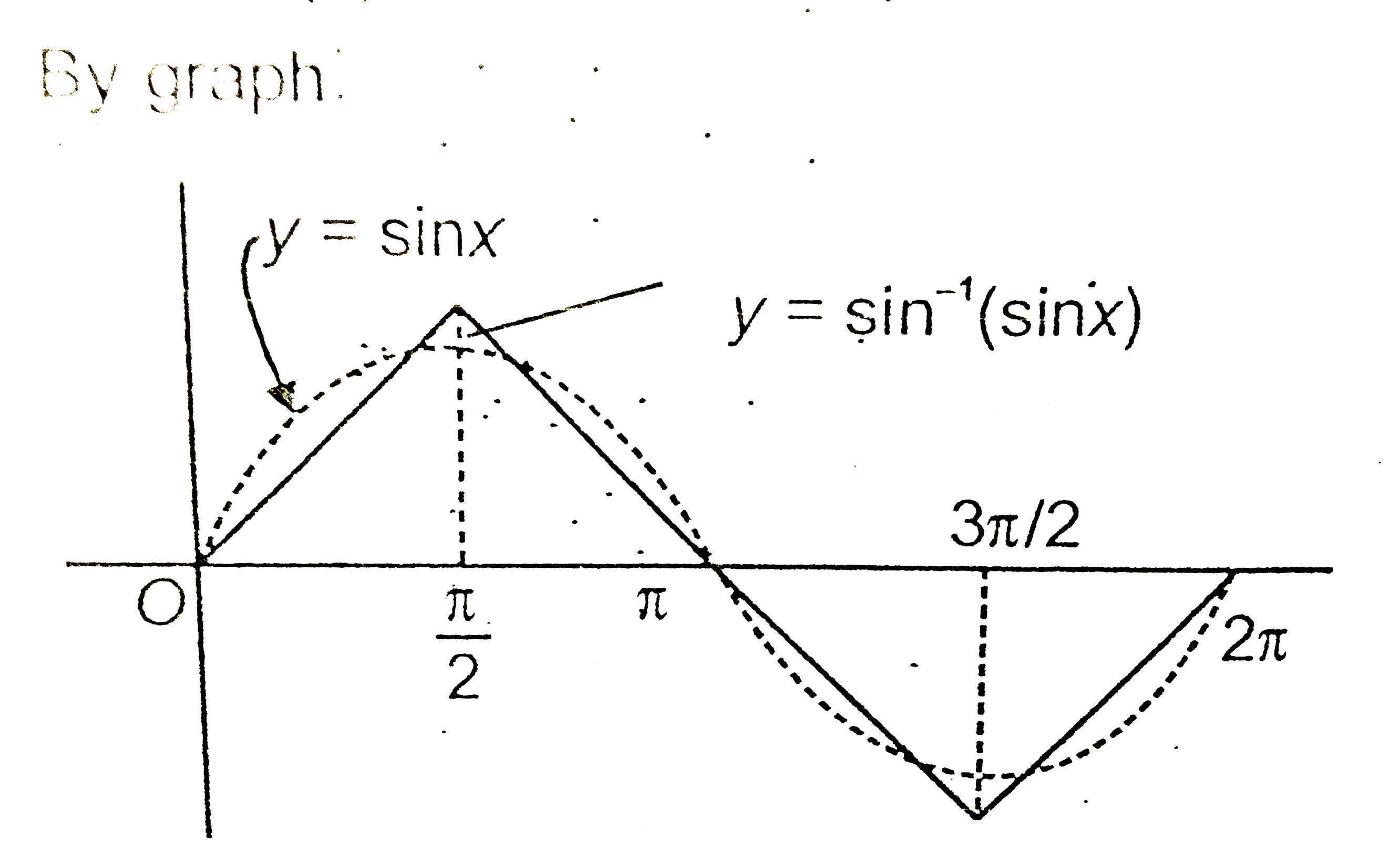
Option 4 is correct.
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - TRY YOURSELF
21 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - ASSIGNMENT (SECTION - A)(OBJECTIVE TYPE QUESTIONS (ONE OPTION IS CORRECT))
45 Videos
- INTEGRALSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - INTEGRALSEXERCISE - Try yourself
50 Videos
- LIMITS AND DERIVATIVES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LIMITS AND DERIVATIVES EXERCISE - Section - j
3 Videos
Similar Questions
Solutions of sin−1(sinx)=sinx are if x∈(0,2π)
View SolutionSolve sin−1(sin6x)=x,x∈[0,π]
View SolutionNumber of solutions of the equation 2sin3x+6sin2x−sinx−3=0 in (0,2π), are
View SolutionFind the solution set for , 4sin2x−8sinx+3≤0 where x∈[0,2π]
View SolutionIf y=sin−1(sinx), then dydx at x=π2 is
View SolutionThe number of solutions of the equation sinx.Sin2x.Sin3x=1 in [0,2π] is
View SolutionSolve cos−1(cosx)>sin−1(sinx),x∈[0,2π]
View SolutionFind the number of solutions of the equations
(sinx−1)3+(cosx−1)3+(sinx)3=(2sinx+cosx−2)3 in (0,2π).
View SolutionThe solution of sin−1|sinx|=√sin−1|sinx| is
View SolutionThe total number of solution of the equation sin4x+cos4x=sinxcosx in [0,2π] is :
View Solution
