Prove that: sin−1(12)13+cos−145+tan−1(63)16=π
Video Solution
Text Solution
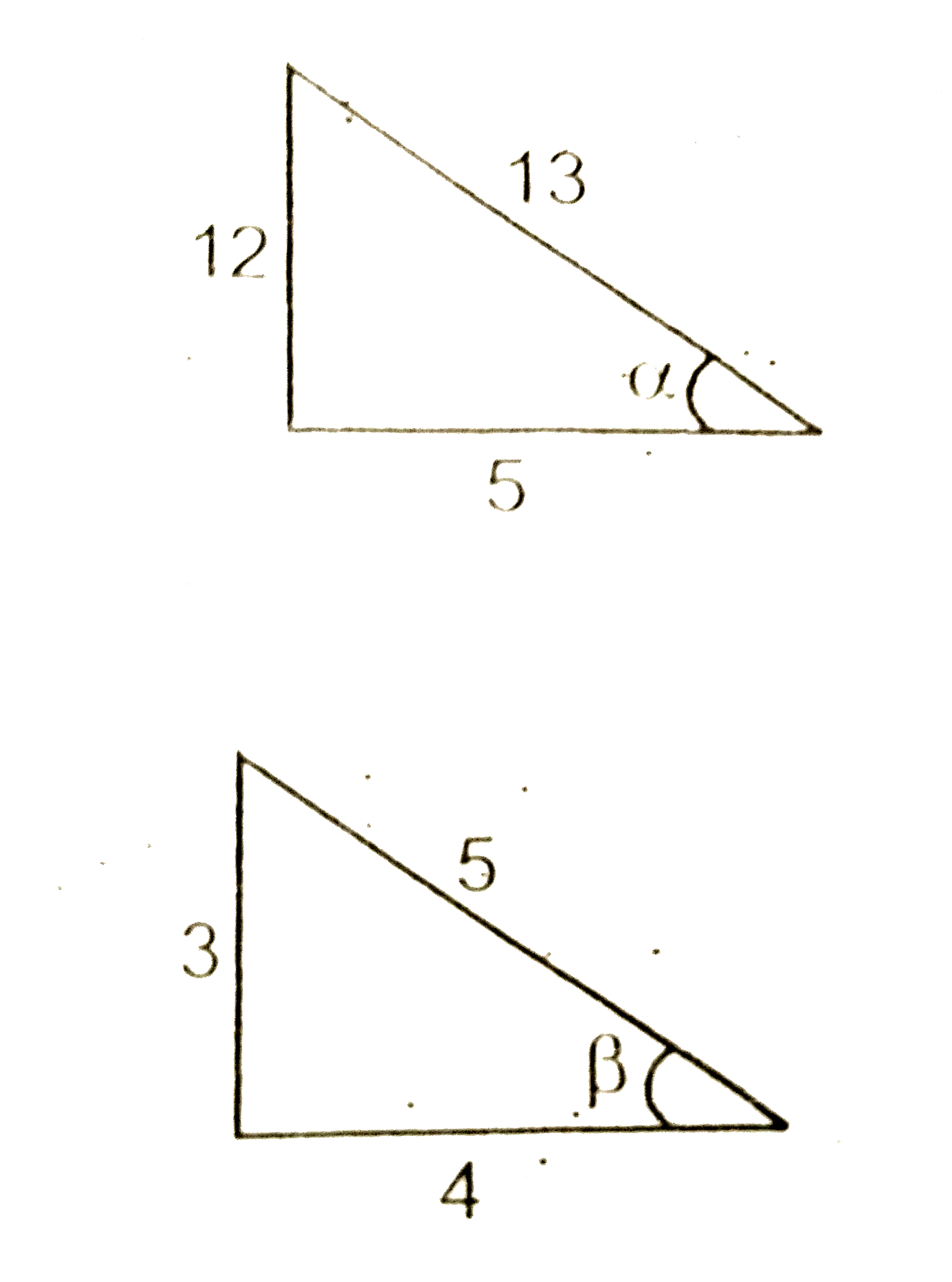
Let sin−1(1213)=α,cos−1(45)=β,tan−1(6316)=γ
⇒sinα=1213,cosβ=45,tanγ=6316
⇒tanα=125
andtanβ=34
Now, α=tan−1(125)&β=tan−1(34)
Here, xy=125×34=95>1
∴ We cannot use tan−1x+tan−1y=tan−1(x+y1−xy),xy>1
Consider, tan(α+β)=tanα+tanβ1−tanαtanβ
=125+341−125×34
=48+1520−36
=−6316
=−tany
∵tanα=125&tanβ=34
⇒tanαtanβ>1
sinαsinβcosαcosβ>1
⇒sinαsinβ>cosαcosβ(as cosαcosβ>0)
⇒cos(α−β)<0
π2<α+β<π
∴tan(α+β)=−tanγ
α+β≠−γas α+β∈(π2,π)
⇒tan(α+β)=tan(π−γ)
⇒α+β=π−γ
⇒α+γ+β=π
⇒sin−1(1213)+cos−1(45)+tan−1(6316)=π
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBook:AAKASH INSTITUTE ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:TRY YOURSELF
Explore 21 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:AAKASH INSTITUTE ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:ASSIGNMENT (SECTION - A)(OBJECTIVE TYPE QUESTIONS (ONE OPTION IS CORRECT))
Explore 45 Videos
- INTEGRALSBook:AAKASH INSTITUTE ENGLISHChapter:INTEGRALSExercise:Try yourself
Explore 50 Videos
- LIMITS AND DERIVATIVES Book:AAKASH INSTITUTE ENGLISHChapter:LIMITS AND DERIVATIVES Exercise:Section - j
Explore 3 Videos
Similar Questions
Show that sin−1(12)13+cos−145+tan−1(63)16=π.
View SolutionProve that : sin−1(513)+cos−1(35)=tan(−1)(6316)
View SolutionShow that sin−1(513)+cos−1(35)=tan−1(6316).
View SolutionColumn I, Column II sin−145+2tan−113= , p. π6 sin−1(12)13+cos−145+tan−1(63)16= , q. π2 If A=tan−1(x√3)2λ−xandB=tan−1(2x−λλ√3) then the value of a−Bis , r. π4 tan−117+2tan−113= , s. π
View SolutionProve that:cos−1(1213)+sin−1(35)=sin−1(5665)
View SolutionProve that:cos−1(1213)+sin−1(35)=sin−1(5665)
View SolutionProve that: sin−1(45)+sin−1(513)+sin−1(1665)=π2
View SolutionProve that: sin−1(45)+sin−1(513)+sin−1(1665)=π2
View SolutionProve that: cos−145+cos−1(12)13=cos−1(33)65
View SolutionProve that : 4(sin−1(1√10)+cos−1(2√5))=π
View Solution