Calculate the maximum energy that a β particle can have in the following decay:
.8O19→.9F19+.−1e0+¯ν
Given, m(.8O19)=19.003576u,m(.9F19)=18.998403u,m(.−1e0)=0.000549u
The correct Answer is:4.3049 MeV
To solve the problem of calculating the maximum energy that a beta particle can have in the decay of 8O19 to 9F19+−1e0+¯ν, we will follow these steps:
Step 1: Identify the masses involved in the decay
We are given the following masses:
- Mass of 8O19 (Oxygen-19): m(8O19)=19.003576u
- Mass of 9F19 (Fluorine-19): m(9F19)=18.998403u
- Mass of the beta particle (electron): m(−1e0)=0.000549u
Step 2: Calculate the mass defect (Δm)
The mass defect is calculated as the difference between the mass of the reactant and the total mass of the products. The equation for mass defect is:
Δm=m(8O19)−(m(9F19)+m(−1e0))
Substituting the values:
Δm=19.003576u−(18.998403u+0.000549u)
Calculating this gives:
Δm=19.003576u−19.000952u=0.002624u
Step 3: Calculate the Q-value of the reaction
The Q-value, which represents the energy released in the decay, can be calculated using the mass defect and the energy-mass equivalence relation:
Q=Δm⋅c2
Where c2 is given as 931.5MeV/u. Thus,
Q=0.002624u⋅931.5MeV/u
Calculating this gives:
Q=2.448MeV
Step 4: Determine the maximum energy of the beta particle
In beta decay, the maximum energy of the beta particle (electron) is equal to the Q-value of the decay, since the neutrino carries away negligible energy. Therefore, the maximum energy of the beta particle is:
Emax=Q=2.448MeV
Final Answer
The maximum energy that the beta particle can have in this decay is approximately 2.448 MeV.
---
We are given the following masses:
- Mass of 8O19 (Oxygen-19): m(8O19)=19.003576u
- Mass of 9F19 (Fluorine-19): m(9F19)=18.998403u
- Mass of the beta particle (electron): m(−1e0)=0.000549u
The mass defect is calculated as the difference between the mass of the reactant and the total mass of the products. The equation for mass defect is:
Δm=m(8O19)−(m(9F19)+m(−1e0))
Substituting the values:
Δm=19.003576u−(18.998403u+0.000549u)
Calculating this gives:
Δm=19.003576u−19.000952u=0.002624u
The Q-value, which represents the energy released in the decay, can be calculated using the mass defect and the energy-mass equivalence relation:
Q=Δm⋅c2
Where c2 is given as 931.5MeV/u. Thus,
Q=0.002624u⋅931.5MeV/u
Calculating this gives:
Q=2.448MeV
In beta decay, the maximum energy of the beta particle (electron) is equal to the Q-value of the decay, since the neutrino carries away negligible energy. Therefore, the maximum energy of the beta particle is:
Emax=Q=2.448MeV
The maximum energy that the beta particle can have in this decay is approximately 2.448 MeV.
Topper's Solved these Questions
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - Assignment Section A Objective (One option is correct )
52 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - Assignment Section B Objective (One option is correct )
10 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
13 Videos
Similar Questions
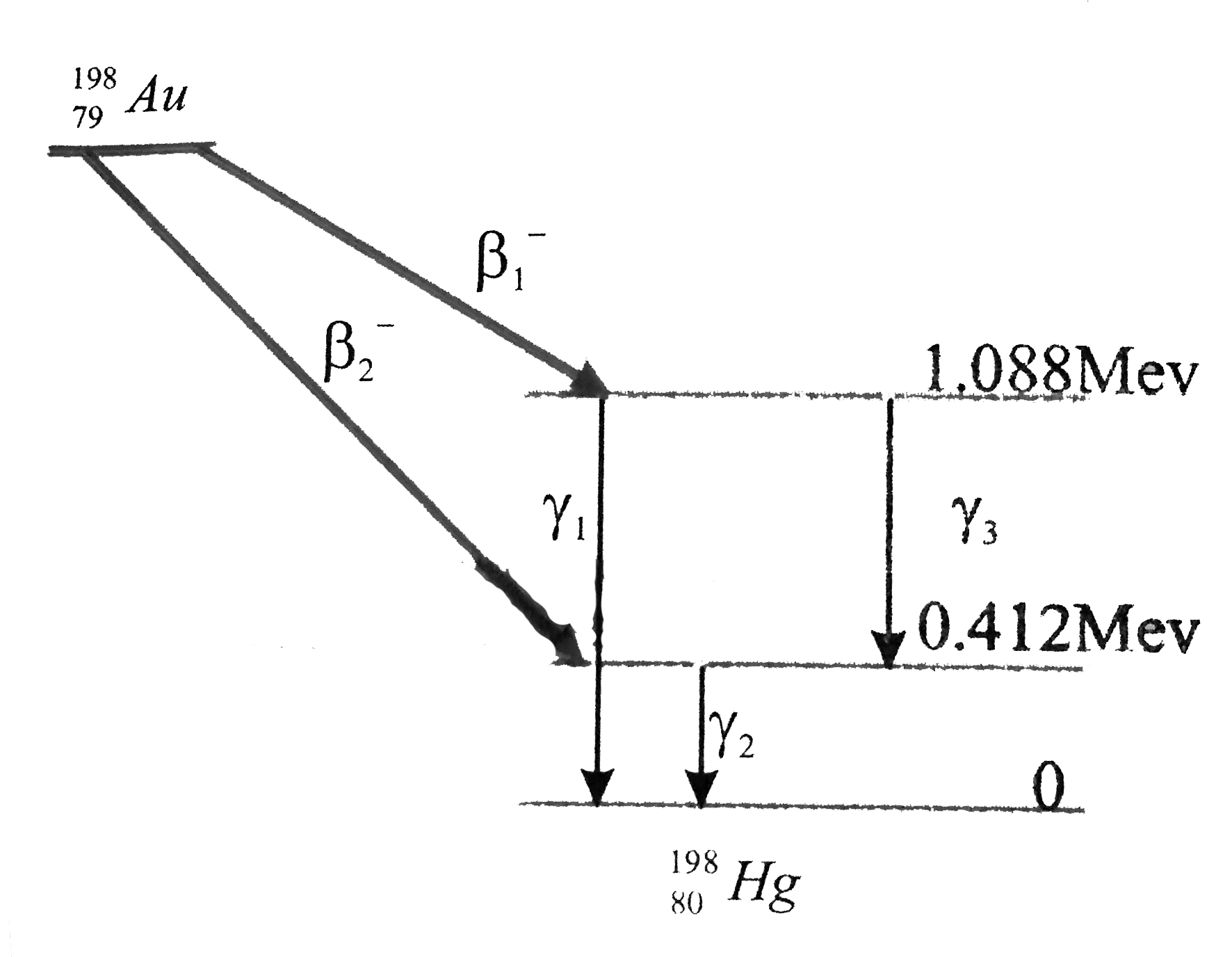
Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 14.6. You are given that m(.198Au)=197.968233u,m(.198Hg)=197.966760u
View SolutionWhich of the two rational numbers is greater in each of the following pairs?
(i) 3−8 or 0, (ii) 119 or 0
View SolutionCalculate the Q-value in the following decays:
(a) ^19O→19F+e+→v.
(b) ^25A1→25Mg+e++v.
The atomic masses needed are as follows :
^19O19.003576u
^19F18.998403u
^25A124.990432u
^25Mg24.985839u
View SolutionFind the absolute maximum and the absolute minimum values of the following function in the given intervals: f(x)=(x−2)√x−1 in [1,9]
View SolutionFind the absolute maximum and the absolute minimum values of the following function in the given intervals: f(x)=(x−2)√x−1 in [1,9]
View SolutionShow the following numbers on the number line.
(a) 0.2 (b) 1.9 (c) 1.1 (d) 2.5
View SolutionAssuming that four hydrogen atom combine to form a helium atom and two positrons, each of mass 0.00549u, calculate the energy released. Given m(.1H1)=1.007825u,m(.2He4)=4.002604u.
View SolutionShow that (.5526Fe) may electron capture, but not β+ decay.
Masses given are M(.5526Fe)=54.938298amu,
M(.5525Mn)=54.938050amu,m(e)=0.000549amu.
View SolutionCalculate binding energy of oxygen nucleus (168O) from the data given below:
Mass of a proton mp= 1.007825u
Mass of neutron mn= 1.008665u
Mass of (168O)mo= 15.994915 u
View SolutionDetermine the mass of an electron if for an electron em=1.759×108Cg−1ande=1.6021×10−19C
View Solution
