A particle of mass is confined to a narrow tube of length L.
(a) Find the wavelengths of the de-Brogile wave which will resonate in the tube.
(b) Calculate the corresponding particle moments. and
(c) Calculate the corresponding energies.
(a)The de-Broglie waves will resonate with a node at each end of the tube.
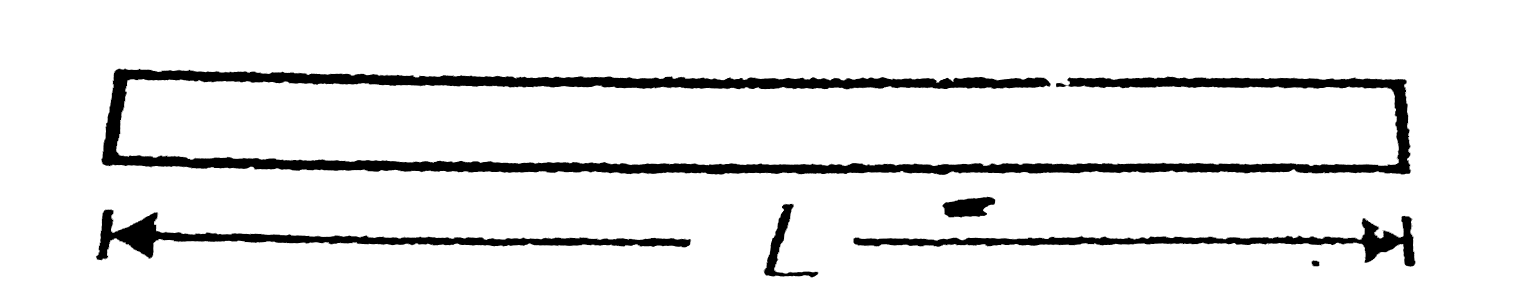
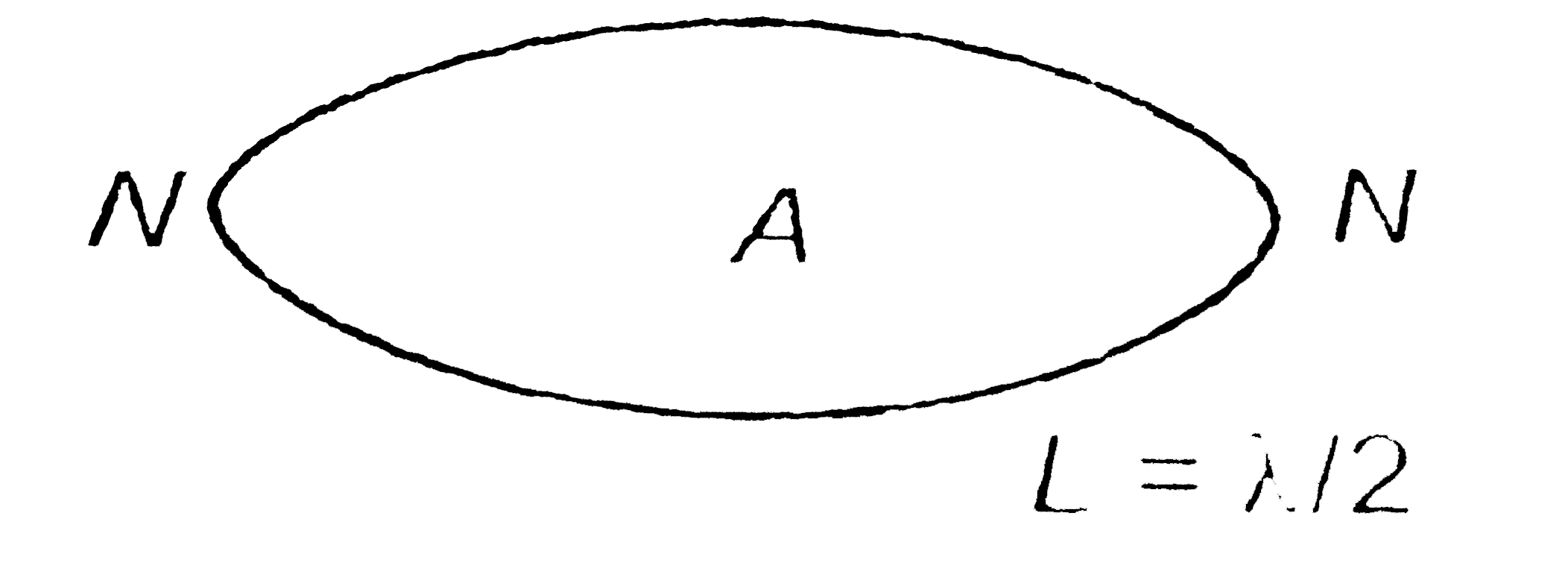
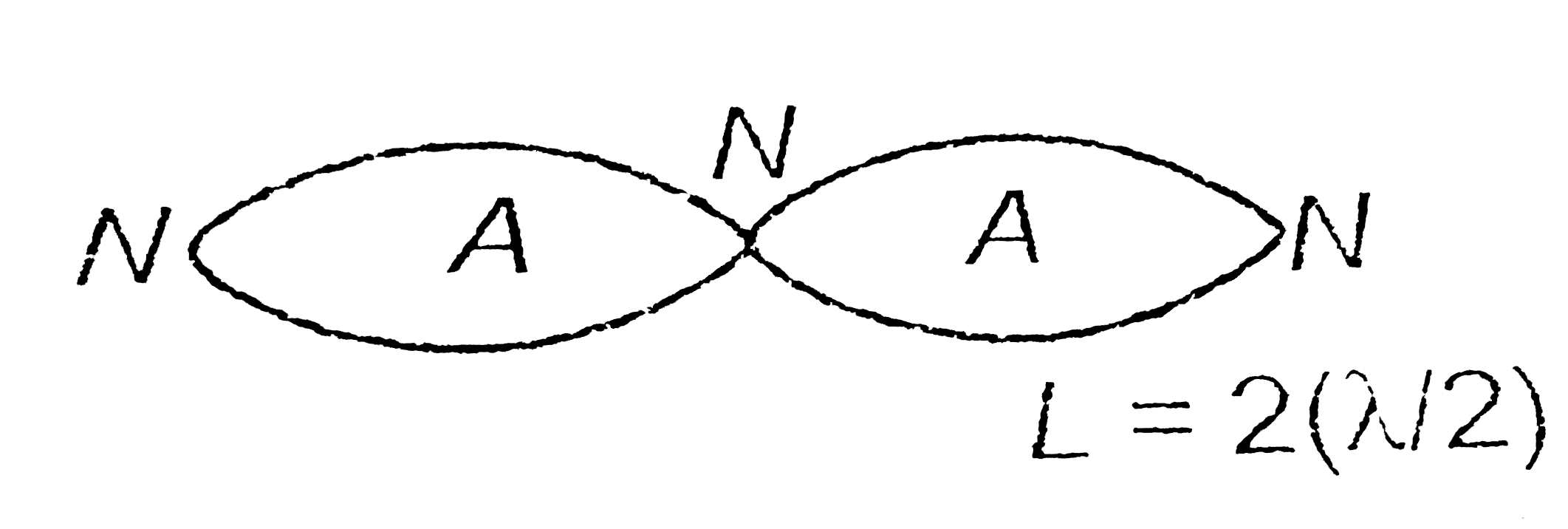
A few of the possible resonance forms are as follows :
λn=2Ln,n=1,2,3……
(b)Since de-Broglie wavelengths are λn=hpn
pn=hλn
=nh2L, n=1,2,...
(c ) The kinetic energy of the particles are Kn=p2n2m
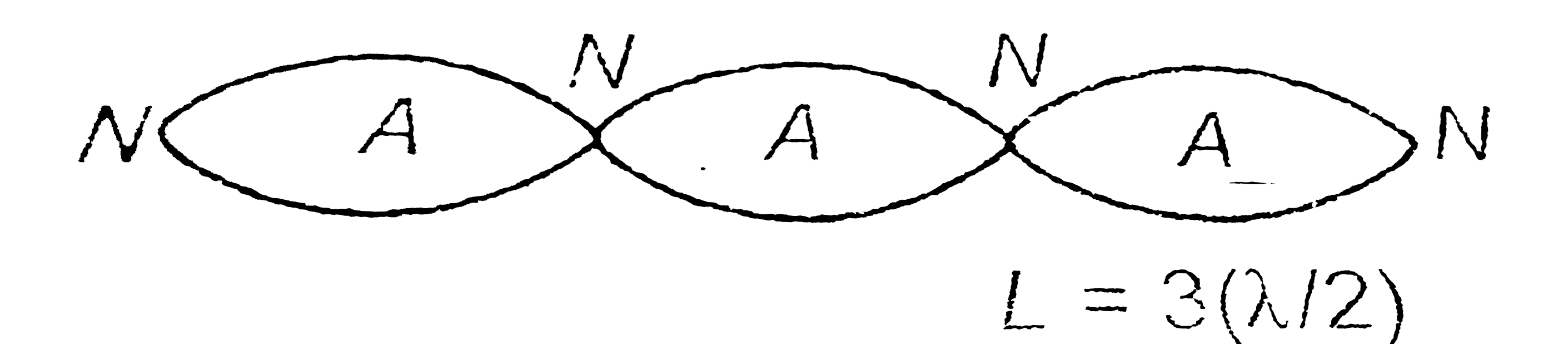
=n2h28L2mn=1,2,3......
Topper's Solved these Questions
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - Try Yourself
24 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION A Objective (One option is correct )
35 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section-J) (Aakash Chailengers Questions)
2 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
Similar Questions
A material particle with a rest mass mo is moving with a velocity of light c. Then, the wavelength of the de Broglie wave associated with it is
View Solutionwavelength of Bullet. Calculate the de-Brogli wavelength of a 5.00 g bullet that is moving at 340 m/s will it exhibite wave like particle?
View Solution
Knowledge Check
A particle is moving three times as fast as an electron. The ratio of the de- Broglie wavelength of the particle to that of the electron is 1.813×10−4. Calculate the particle's mass and identify the particle. Mass of electron =9.11×10−31kg.
A1.67×10−27kgB1.67×10−31kgC1.67×10−19kgD1.67×10−14kg
Calculate the momentum of a particle which has de Broglie wavelength of 0.1 nm.
View SolutionA particle is moving three times as fast as an electron. The ratio of the de- Broglie wavelength of the particle to that of the electron is 1.813×10−4. Calculate the particle's mass and identify the particle. Mass of electron =9.11×10−31kg.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19 C.
Q. If the mass of the particle is m=1.0×10−30kg and α=6.6nm, the energy of the particle in its ground state is closest to
View SolutionWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19 C.
Q. The allowed energy for the particle for a particular value of n is proportional to
View SolutionWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19C
Q. The speed of the particle that can take discrete values is proportional to
View Solution
