(a)Use the Bohr model to determine the ionization energy of the He+ ion, which has a single electron. (b)Also calculate the maximum wavelength a photon can have to cause ionization.
To solve the problem, we will break it down into two parts as given in the question.
Part (a): Determine the ionization energy of the He+ ion using the Bohr model.
1. Understanding the Ionization Energy Formula:
The ionization energy (E_i) for a hydrogen-like atom can be calculated using the formula:
\(
E_i = -13.6 \, \text{eV} \times Z^2 \times \left( \frac{1}{n_i^2} - \frac{1}{n_f^2} \right)
\)
where:
- \( Z \) is the atomic number,
- \( n_i \) is the initial principal quantum number,
- \( n_f \) is the final principal quantum number (for ionization, \( n_f \) approaches infinity).
2. Identifying Values for He+:
- For the helium ion He+, the atomic number \( Z = 2 \).
- The electron in He+ is in the ground state, so \( n_i = 1 \).
- For ionization, \( n_f \) approaches infinity.
3. Substituting Values into the Formula:
\(
E_i = -13.6 \, \text{eV} \times 2^2 \times \left( \frac{1}{1^2} - \frac{1}{\infty^2} \right)
\)
\(
E_i = -13.6 \, \text{eV} \times 4 \times \left( 1 - 0 \right)
\)
\(
E_i = -54.4 \, \text{eV}
\)
4. Calculating the Ionization Energy:
The ionization energy is the absolute value of \( E_i \):
\(
\text{Ionization Energy} = 54.4 \, \text{eV}
\)
Part (b): Calculate the maximum wavelength a photon can have to cause ionization.
1. Using the Energy-Wavelength Relation:
The energy of a photon is related to its wavelength by the equation:
\(
E = \frac{hc}{\lambda}
\)
where:
- \( h \) is Planck's constant (\( 6.626 \times 10^{-34} \, \text{Js} \)),
- \( c \) is the speed of light (\( 3 \times 10^8 \, \text{m/s} \)),
- \( \lambda \) is the wavelength.
2. Rearranging the Equation to Solve for Wavelength:
\(
\lambda = \frac{hc}{E}
\)
3. Converting Ionization Energy to Joules:
Since \( 1 \, \text{eV} = 1.6 \times 10^{-19} \, \text{J} \):
\(
E = 54.4 \, \text{eV} \times 1.6 \times 10^{-19} \, \text{J/eV} = 8.704 \times 10^{-18} \, \text{J}
\)
4. Substituting Values into the Wavelength Equation:
\(
\lambda = \frac{(6.626 \times 10^{-34} \, \text{Js}) \times (3 \times 10^8 \, \text{m/s})}{8.704 \times 10^{-18} \, \text{J}}
\)
5. Calculating the Wavelength:
\(
\lambda \approx \frac{1.9878 \times 10^{-25}}{8.704 \times 10^{-18}} \approx 2.28 \times 10^{-8} \, \text{m} = 22.8 \, \text{nm}
\)
Final Answers:
- (a) The ionization energy of the He+ ion is 54.4 eV.
- (b) The maximum wavelength a photon can have to cause ionization is 22.8 nm.
The ionization energy (E_i) for a hydrogen-like atom can be calculated using the formula:
\(
E_i = -13.6 \, \text{eV} \times Z^2 \times \left( \frac{1}{n_i^2} - \frac{1}{n_f^2} \right)
\)
where:
- \( Z \) is the atomic number,
- \( n_i \) is the initial principal quantum number,
- \( n_f \) is the final principal quantum number (for ionization, \( n_f \) approaches infinity).
- For the helium ion He+, the atomic number \( Z = 2 \).
- The electron in He+ is in the ground state, so \( n_i = 1 \).
- For ionization, \( n_f \) approaches infinity.
\(
E_i = -13.6 \, \text{eV} \times 2^2 \times \left( \frac{1}{1^2} - \frac{1}{\infty^2} \right)
\)
\(
E_i = -13.6 \, \text{eV} \times 4 \times \left( 1 - 0 \right)
\)
\(
E_i = -54.4 \, \text{eV}
\)
The ionization energy is the absolute value of \( E_i \):
\(
\text{Ionization Energy} = 54.4 \, \text{eV}
\)
The energy of a photon is related to its wavelength by the equation:
\(
E = \frac{hc}{\lambda}
\)
where:
- \( h \) is Planck's constant (\( 6.626 \times 10^{-34} \, \text{Js} \)),
- \( c \) is the speed of light (\( 3 \times 10^8 \, \text{m/s} \)),
- \( \lambda \) is the wavelength.
\(
\lambda = \frac{hc}{E}
\)
Since \( 1 \, \text{eV} = 1.6 \times 10^{-19} \, \text{J} \):
\(
E = 54.4 \, \text{eV} \times 1.6 \times 10^{-19} \, \text{J/eV} = 8.704 \times 10^{-18} \, \text{J}
\)
\(
\lambda = \frac{(6.626 \times 10^{-34} \, \text{Js}) \times (3 \times 10^8 \, \text{m/s})}{8.704 \times 10^{-18} \, \text{J}}
\)
\(
\lambda \approx \frac{1.9878 \times 10^{-25}}{8.704 \times 10^{-18}} \approx 2.28 \times 10^{-8} \, \text{m} = 22.8 \, \text{nm}
\)
- (a) The ionization energy of the He+ ion is 54.4 eV.
- (b) The maximum wavelength a photon can have to cause ionization is 22.8 nm.
Topper's Solved these Questions
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - Try Yourself
24 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION A Objective (One option is correct )
35 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section-J) (Aakash Chailengers Questions)
2 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
Similar Questions
Determine the minimum wavelength of a photon the can cause ionization of He ^(+) ion.
View SolutionCalculate the wavelength of a photon in Angstroms having an energy of 1 electron-volt.
View SolutionThe work function of the metal A is equal to the ionization energy of the hydrogen atom in the first excited state. The work function of the metal B is equal to the ionization energy of He+ ion in the second orbit. Photons of the same energy E are incident on both A and B the maximum kinetic energy of photoelectrons emitted from A is twice that of photoelectrons emitted from B. Value of E (in eV) is
View Solution(a) Using the Bohr's model, calculate the speed of the electron in a hydrogen atom in the n=1,2 and 3 levels. (b) Calculate the orbital period in each of these levels.
View SolutionWith the help of Bohr 's model , calculate the second ionisation energy of helium (energy required to remove the electron from He⊕
View SolutionWhen an atom X absorbs radiation with a photon energy than the ionization energy of the atom, the atom is ionized to generate an ion X+ and the electron (called a photoelectron) is ejected at the same time. In this event, the energy is conserved as shown in Figure 1, that is,
Photon energy (h)=ionization energy (IE) of X+ kinetic energy of photoelectron.
When a molecule, for example, H2, absorbs short-wavelength light, the photoelectron is ejected and an H2, ion with a variety of vibrational states is produced. A photoelectron spectrum is a plot of the number of photoelectrons as a function of the kinetic energy of the photoelectrons. Figure-2 shows a typical photoelectron spectrum when H2 in the lowest vibrational level is irradiated by monochromatic light of 21.2eV. No photoelectrons are detected above 6.0eV. (eV is a unit of energy and 1.0eV is equal to 1.6×10−19J)
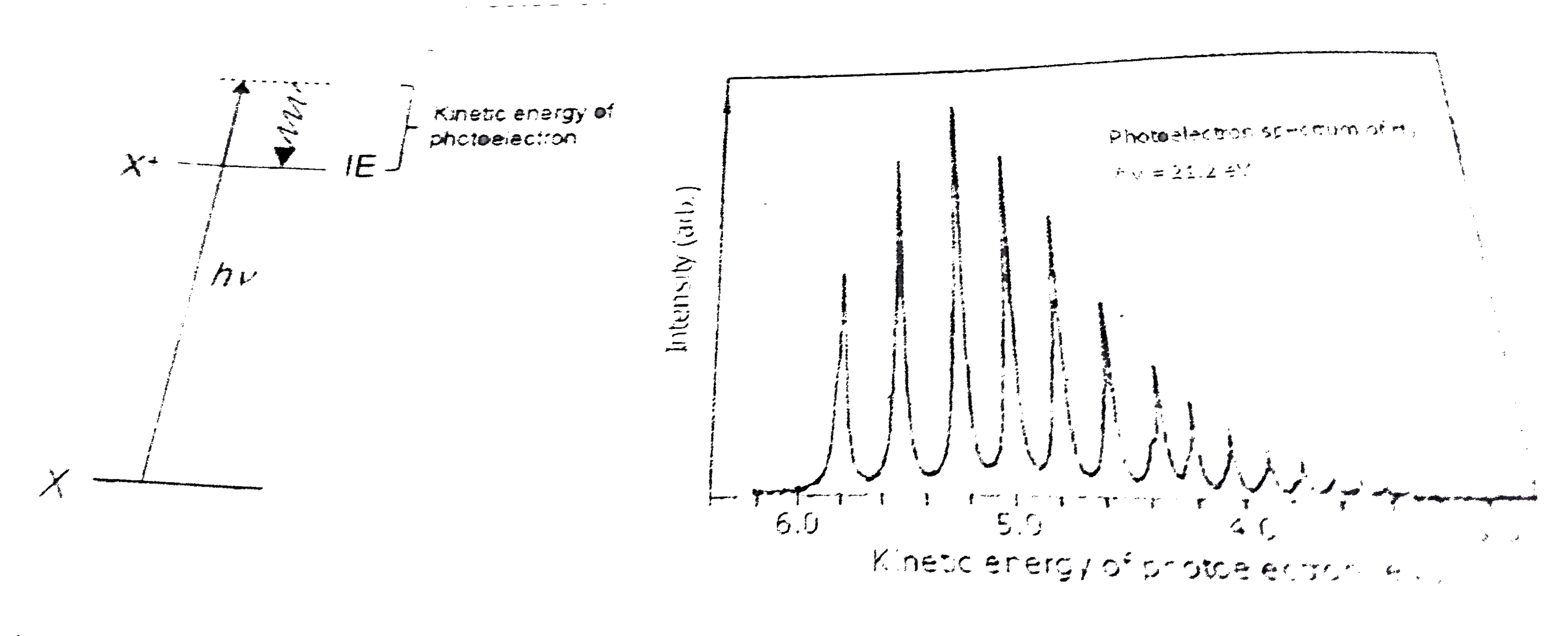
Figure 1 Schematic diagram of photoelectron spectroscopy.
Figure 2 Photoelectron spectrum of H2. The energy of the incident light is 21.2eV
Considering an energy cycle, determine––––––––––– the bond energy ED(eV) of H+2 to the first decimal place. If you were unable to determine the values for EB and EC, then use 15.0eV and 5.0eV for EB and EC, respectively.
View SolutionA photon and an electron have the same de Broglie wavelength. Which has greater total energy? Explain
View SolutionIf out of two given elements A and B, A has a higher ionization energy than B, which element is expected to be more electronegative A or B ?
View SolutionA certain species of ionized atoms produces emission line spectral accorduing to the Bohr's model. A group of lines in the spectrum is forming a series in which in the shortest wavelength is 22.79nm and the longest wavelength is 41.02nm. The atomic number of atom is Z.
Based on above information, answer the following question:
The series belongs to
View SolutionDetermine the degree if ionization and pH of 0.05M of ammonia solution. The ionization constant of ammonia can be taken from Table 7.7. Also calculate the ionization constant of the conjugate acid of ammonia.
View Solution
