What would be the charge in radius of nth orbit, if the mass of electron reduces to half of its original value ?
To solve the problem of finding the change in the radius of the nth orbit when the mass of the electron is reduced to half of its original value, we can follow these steps:
1. Understand the Relationship:
The radius of the nth orbit in a hydrogen atom (or similar systems) is given by the formula:
rn=n2h24π2ke2m
where:
- rn is the radius of the nth orbit,
- n is the principal quantum number,
- h is Planck's constant,
- k is Coulomb's constant,
- e is the charge of the electron,
- m is the mass of the electron.
2. Identify the Inverse Proportionality:
From the formula, we can see that the radius rn is inversely proportional to the mass m of the electron. This means:
rn∝1m
3. Change in Mass:
According to the problem, the mass of the electron is reduced to half of its original value:
m′=m2
4. Substituting the New Mass:
If we substitute the new mass into the relationship, we have:
r′n=n2h24π2ke2m′=n2h24π2ke2(m2)=2n2h24π2ke2m=2rn
Thus, the new radius r′n becomes twice the original radius rn.
5. Conclusion:
Therefore, if the mass of the electron is reduced to half, the radius of the nth orbit will be doubled:
r′n=2rn
Final Answer:
The radius of the nth orbit would be doubled if the mass of the electron reduces to half of its original value.
---
The radius of the nth orbit in a hydrogen atom (or similar systems) is given by the formula:
rn=n2h24π2ke2m
where:
- rn is the radius of the nth orbit,
- n is the principal quantum number,
- h is Planck's constant,
- k is Coulomb's constant,
- e is the charge of the electron,
- m is the mass of the electron.
From the formula, we can see that the radius rn is inversely proportional to the mass m of the electron. This means:
rn∝1m
According to the problem, the mass of the electron is reduced to half of its original value:
m′=m2
If we substitute the new mass into the relationship, we have:
r′n=n2h24π2ke2m′=n2h24π2ke2(m2)=2n2h24π2ke2m=2rn
Thus, the new radius r′n becomes twice the original radius rn.
Therefore, if the mass of the electron is reduced to half, the radius of the nth orbit will be doubled:
r′n=2rn
The radius of the nth orbit would be doubled if the mass of the electron reduces to half of its original value.
Topper's Solved these Questions
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - Try Yourself
24 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION A Objective (One option is correct )
35 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section-J) (Aakash Chailengers Questions)
2 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
Similar Questions
Knowledge Check
The radius of nth orbit rn in the terms of Bohr radius (a0) for a hydrogen atom is given by the relation
Ana0B√na0Cn2a0Dn3a0
It is known that atom contain protons, neutrons and electrons. If the mass of neutron is assumed to half of its original value whereas that of proton is assumed to be twice of its original value then the atomic mass of C146 will be :
View SolutionIt is known that atom contain protons. Neutrons and electrons. If the mass of neutron is assumed to half of its orginal value where as that of proton is assumed to be twice of its original value then the atomic mass of .146C will be :-
View SolutionIt is known that atom contain protons. Neutrons and electrons. If the mass of neutron is assumed to half of its orginal value where as that of proton is assumed to be twice of its original value then the atomic mass of .146C will be :-
View SolutionWhat is the radius of the 4th orbit of He+
View SolutionA wire of length l has a resistance R. If half of the length is stretched to make the radius half of its original value, then the final resistance of the wire is
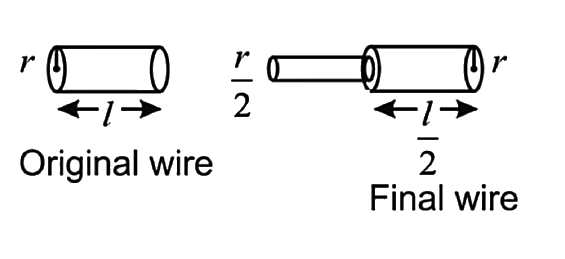
View SolutionIf an orbital electron of the hydrogen atom jumps from the groud state to a higher energy state, its orbital value where its velcoity is reduced to half its initial value.. If the radius of the electron orbit in the ground state is r, then the radius of the new orbit would be:
View SolutionWhat would be the change in tangential velocity of an electron, if it remains in same orbit and electronic charge is doubled ?
View Solution
