The value of apparent angles of dip at two places measured in two mutually perpendicular planes are deg30 and deg45. The true angle of dip at the place is

Video Solution

Text Solution

Verified by Experts

Let $ϕ$ be the true angle of dip and $ϕ_{1}, ϕ_{2}$ be the apparent angles of dip in two mutually perpendicular planes such that $ϕ_{1} = 30^{\circ}$ and $ϕ_{2} = 45^{\circ} ϕ = ?$
Consider the figure shown below

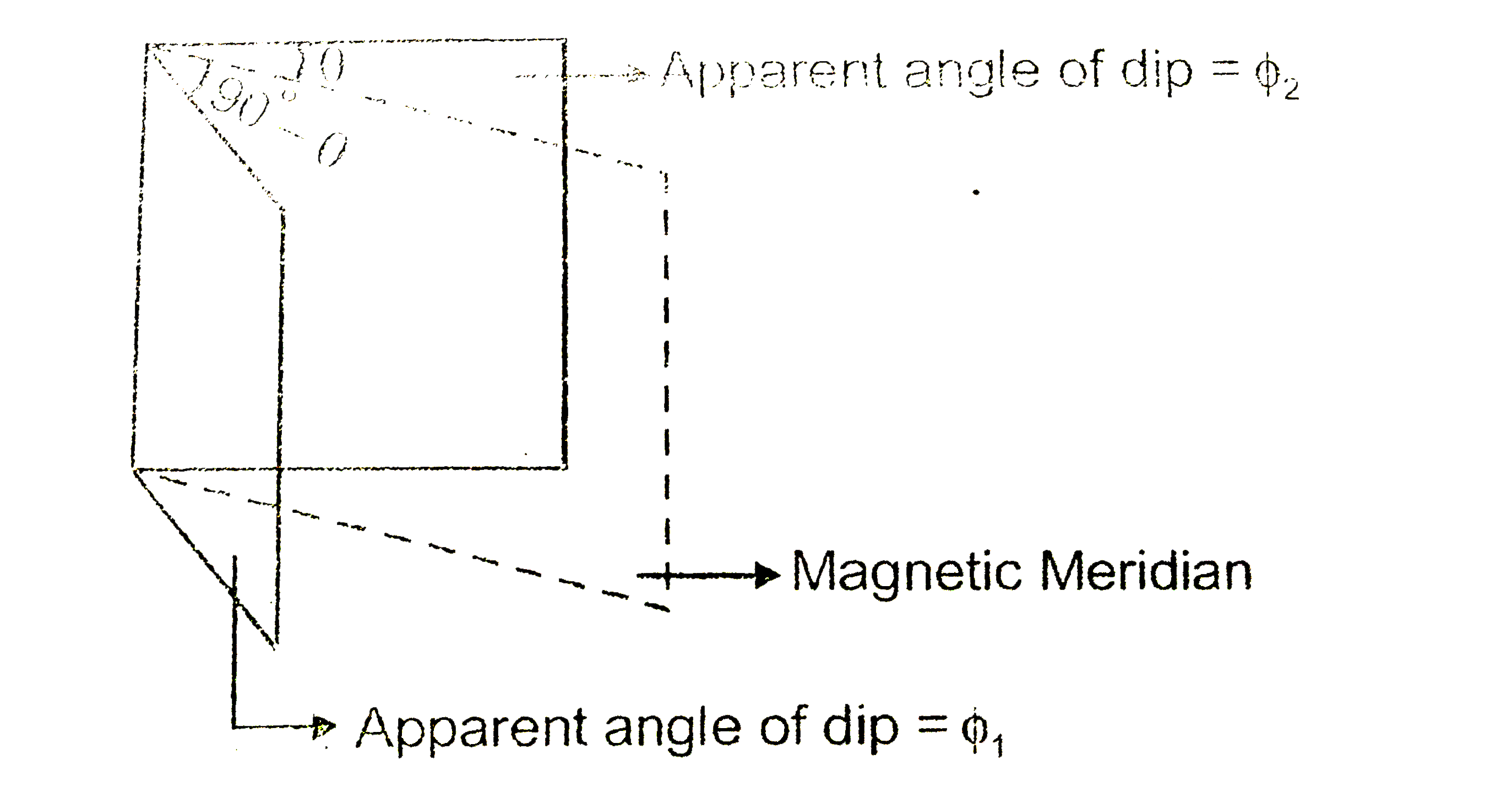
If one vertical plane is at angle $θ$ with magnetic meridian , the other vertical plane makes angle $90^{\circ} - θ$ with the magnetic meridian .
The apparent angle of dip is related to true angle of dip as
$\tan ϕ' = \frac{\tan ϕ}{\cos θ}$
So, we can write
${\tan ϕ}_{1} = \frac{\tan ϕ}{\cos θ} ... (i)$
and ${\tan ϕ}_{2} = \frac{\tan ϕ}{\sin θ} ... (i i)$
As we know that
$\sin^{2} θ + \cos^{2} θ = 1$
So , we get
$\frac{\tan^{2} ϕ}{\tan^{2} ϕ_{1}} + \frac{\tan^{2} ϕ}{\tan^{2} ϕ_{2}} = 1$
$\Rightarrow \cot^{2} ϕ_{1} + \cot^{2} ϕ_{2} = \cot^{2} ϕ$
Plugging in the values of $ϕ_{1}$ and $ϕ_{2}$ , we get
$\cot^{2} 30^{\circ} + \cot^{2} 45^{\circ} = \cot^{2} ϕ$
$\Rightarrow \cot^{2} ϕ = 3 + 1$
= 4
$\cot ϕ = 2$
$ϕ = \cot^{- 1} (2)$
= $\frac{\tan^{- 1} (1)}{2}$ .

Updated on:21/07/2023

What is the angle of dip at a place where horizontal and vertical components of earth's field are equal?
A $30^{\circ}$
B $75^{\circ}$
C $60^{\circ}$
D $45^{\circ}$
The vertical component of earth's magnetic field at a place is $\sqrt{3}$ times the horizontal component the value of angle of dip at this place is
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $75^{\circ}$